전기기초(소자) AB
V 전압, 전류 (AC1)
B 기준충격절연강도(BIL)
D 전압강하 (LMD)
S 변위전류 (AE)
F 패란티 현상 (QVF)
M 단락전자력 (LMMS)
이상전압 및 대책 (BS)
C 코로나 (AG)(LP)
코로나(임계전압식 유도⁕)
R 저항 임피던스 리액턴()
I 특성임피던스 ()
P 전력 역률
A 무효전력
L 최대전력전달
저항 임피던스 리액턴스 ABR
저항 임피던스 리액턴스
❗저항(R, Resistance)
1️⃣저항의 정의
- 저항은 전류의 흐름을 방해하는 정도를 표시하는 양으로 정의
2️⃣도선의 저항
3️⃣저항에 영향을 주는 요인
1)온도
2)주파수
- 교류의 경우 전류가 표면 가까이 흐르려고 하는데 이러한 성질을 표피효과라고 한다. 그러므로 교류가 직류보다 주파수가 높을수록 저항이 증가
4️⃣고유저항
고유저항이란 단위길이와 단위면적을 가지고 있는 물직의 고유한 저항특성을 의미하며 1[㎡]저항의 크기를 고유저항이라 한다. 기호는 ρ, 단위는 [Ω*m]이다
5️⃣저항률
저항률이란 물질이 가지고 있는 저항특성을 말하며, 단위는[Ω*m]를 사용한다.대표적으로 대지저항률이 있다.
❗도전율(Conductivity)
1️⃣도전율의 정의
고유저항의 역수를 도전율이라 한다
2️⃣IEC의 정의
표준연동(20℃, 길이1m, 1㎟)의 균일 단면을 작는 표준연동의 저항을 1/58[Ω/m-㎟], 밀도 8.89[g/㎤]를 100%로 하여, 이와 비교하면 백분율로 표시한다
3️⃣도전율C[%]와 고유저항ρ사이의 관계식
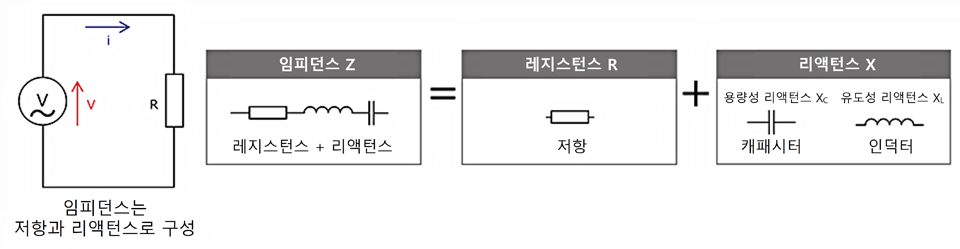
❗임피던스(Z, impedence)
1️⃣임피던스의 정의
- 전류의 흐름을 방해하는 성질로서 교류에서 사용한다
- 저항과 리액턴스의 합으로 나타낸다
- 임피던스는 크기와 위상으로 표현되며, 복소수로 나타낼 수 있습니다.
- 임피던스 Z는 다음과 같이 표현됩니다.
- R: 저항 (Resistance)
- X: 리액턴스 (Reactance)
- XL: 유도 리액턴스 (인덕터에 의한 반작용)
- XC: 용량 리액턴스 (콘덴서에 의한 반작용)
- j: 허수 단위
2️⃣임피던스의 필요성
- 직류회로에서 전류의 흐름을 제한하는 것은 저항뿐
- 교류회로에서 전류를 제한하는 요소에 리액턴스가 추가되어 임피던스의 개념이 필요
- 리액턴스에는
- 인덕턴스(코일)에 의한 유도성 리액턴스
- 정전용량(콘덴서)에 의한 용량성 리액턴스
- 인덕턴스와 정전용량은 전력을 소비하지 않고 단지 전력을 저장했다 방출하는 과정을 되풀이 할 뿐이다
3️⃣%임피던스 (%Z)
1)%임피던스란
- %임피던스는 임피던스의 값을 백분율로 나타낸 것
- 주로 변압기, 모터 등의 전기 기기에서 사용되는 용어로, 기기의 특성을 나타내는 중요한 지표

Vs : 임피던스 전압, Vn : 정격전압
Z : 현재 대상으로 한 회로부분의 임피던스
In : 정격전류, E : 회로전압
2)임피던스 전압
- 2차측을 단락하고 1차측에 정격전류가 흐르도록 인가하는 전압
- 변압기 자체 임피던스를 알고자 할 때 사용
4️⃣%Z가 1,2차 측이 동일한 이유

1)1차측 %임피던스
2)2차측 %임피던스
3)1,2차측 전압, 전류, 임피던스 관계
상기 식을 대입하여 정리하면
❗리액턴스(X, Reactance)
1️⃣유도성 리액턴수(XL)
- 인덕턴스 성분을[옴]의 단위로 나타내는 값
- 인덕턴스는 기호로 L 을 사용하고 단위는 [H](henry)또는 [mH]를 사용한다
- 유도성부하 : 코일
2️⃣용량성 리액턴스(XC)
- 정전용량 성분을 의 단위로 나타낸 값
- 정전용량은 기호로 C를 사용하고 단위는[F](Farad)또는 [μF]
- 용량성부하 : 콘덴서
3️⃣XL, XC의 관계
❗수동소자 능동소자
1️⃣수동소자
- 전력을 소비 축적 방출하는 소자
- 능동적 기능을 하지 못한다
- 저항, 인버터, 커페시터가 있다
2️⃣능동소자
- 작은신호를 넣어 큰 출력 신호로 변화시킬수 있는 소자
- 트랜지스터, 다이오드가 있다.
전기기초(소자) AB
V 전압, 전류 (AC1)
B 기준충격절연강도(BIL)
D 전압강하 (LMD)
S 변위전류 (AE)
F 패란티 현상 (QVF)
M 단락전자력 (LMMS)
이상전압 및 대책 (BS)
C 코로나 (AG)(LP)
코로나(임계전압식 유도⁕)
R 저항 임피던스 리액턴()
I 특성임피던스 ()
P 전력 역률
A 무효전력
L 최대전력전달
저항 임피던스 리액턴스 ABR
저항 임피던스 리액턴스
🌐V0411S25 / ABR
답글 남기기