평형3상회로 ACY
평형3상 회로
3상 평형회로에서 전압 또는 전류의 합은 항상 0이 된다.
- 평형 3상 회로전압의 합이 0이 되는 이유
다음 그림과 같이 3상 평형전압이 인가될때
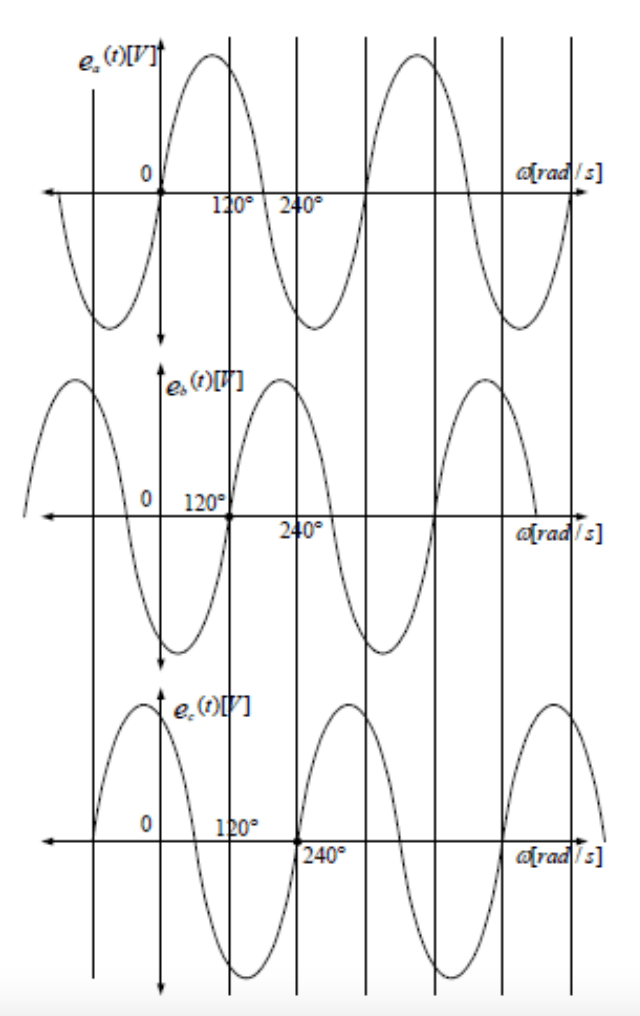
- 삼각함수로 증명
전압순시값을 삼각함수로 표시하면 다음과 같다
\[ e_a=E_m\sin\omega t \]\[ e_b=E_m\sin(\omega t-120) \]\[ e_c=E_m\sin(\omega t -240)\]
각상 전압의 합은
\[ e_a+e_a+e_a\]\[=E_m[\sin\omega t+\sin(\omega t-120)+\sin(\omega t-240)] \]
\[=E_m[\sin\omega t+(\sin\omega t\cos 120-\cos\omega t\sin120)] \]
\[=E_m[\sin\omega t+(-0.5\sin\omega t-0.866\cos\omega t)\]\[+(-0.5\sin\omega t+0.866\cos\omega t)]\]\[ +(\sin\omega t\cos240-\cos\omega t\sin240)]\]\[=0\]
그러므로 각 상 전압의 합은 0이 된다.
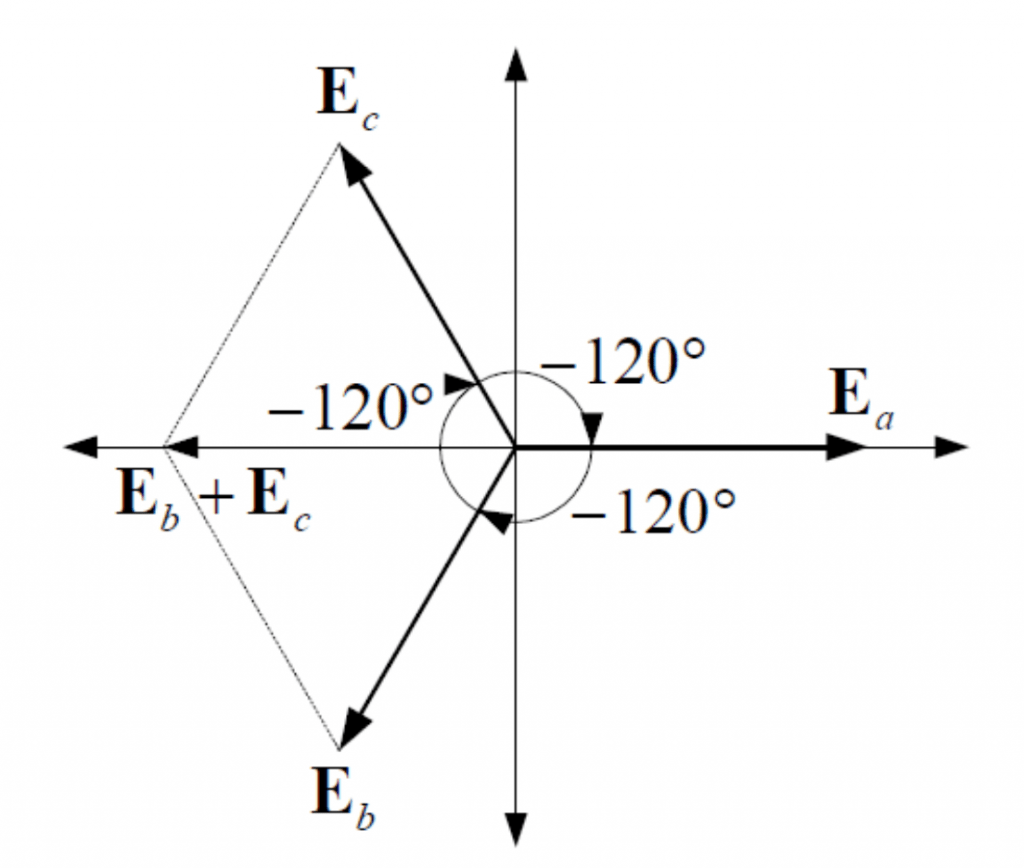
- 극좌표 복소수로 증명
전압 순시갑을 극좌표로 표시하면 다음과 같다.
\[ E_a+E_b+E_c=E+\angle-120+E\angle-240\]\[=E+E(\cos(-120)+j\sin(-120))\]\[+E(\cos(-240)+j\sin(-240))\]\[=E+E(-\frac{1}{2}-j\frac{\sqrt{3}}{2})+E(-\frac{1}{2}+j\frac{\sqrt{3}}{2})=0\]
전기기초(회로) AC
전압원, 전류원
2 회로망의 재정리
3 수동소자의 페이저 해석
4 삼각함수 미분
5 순시값 평균값 실효값
최대전력전달
유도결합회로로
8 평형3상회로
9 비정현파 교류
공진현상
과도현상
필터회로
🌐V1006Z24 / ACY
답글 남기기