순시값 평균값 실효값

전기기초(회로) AC

전압원, 전류원
회로망의 재정리
수동소자의 페이저 해석
–삼각함수 미분
순시값 평균값 실효값
최대전력전달
유도결합회로로
평형3상회로
비정현파 교류
공진현상
–문제1/문제2/문제3/문제4/문제5
과도현상
–문제RL/문제RC
필터회로

상전류 선전류

1️⃣정현파

시간의 변화에 따라서 주기적으로 나타나는 사인파 또는 코사인파
교류 정현파 전압, 전류의 표시

\[v(t) =V_m \sin \omega t \]\[i(t) =I_m \sin \omega t \]

2️⃣최대값

순시값 중에서 가장 큰 값 (Vm, Im)

3️⃣순시값

(Instantaneous Value)

교류전압과 전류는 시간에 따라서 수시로 그 크기와 부호가 바뀌기 때문에 시간의 함수로 표시하는 데 이를 순시전압 및 수시전류라 한다
임의의 어떤 순간의 값

\[ e=E_m \sin\omega t\]\[i=I_m\sin\omega t\]

4️⃣평균값

(Average Value, Root Mean)

주기파에서 1주기 동안의 산술적인 평균값을 나타낸다
정현파 또는 정(+),부(-)값이 존재하는 경우에는 산술적인 평균은 서로 상쇄되어 0이 되므로, 평균값의 정의는 다음과 같다.

\[E_{a} =\frac { 1} { \pi} \int _{ 0} ^{ \pi} { E_m\sin\omega t} dt\]\[ =\frac{E_m}{\pi}[-\cos\omega t]_0^{\pi}\]\[=\frac{E_m}{\pi}[1-(-1)]=\frac{2}{\pi}E_m\]

5️⃣실효값

(Effective value,
RMS: Root Mean Square)

실효값은 직류와 등가할수 있는 양(동일시 취급할수 있는 양)을 교류에서 표현하고자 할 때 사용
실용상 가장 많이 사용되는 값

\[ E_{rms}=\sqrt{\frac{1}{2\pi}\int_{0}^{2\pi}e^2d\omega t }\] \[=\sqrt{\frac{1}{2\pi}\int_{0}^{2\pi}(E_m\sin\omega t)^2d\omega t } \]\[ =\sqrt{\frac{E_m^2}{4\pi}\int_{0}^{2\pi} (1-\cos 2\omega t)d\omega t} \]

\[ =\sqrt{\frac{E_m^2}{4\pi}[\omega t-\frac{1}{2}\sin 2\omega t]_0^{2\pi}}\]\[ =\sqrt{\frac{E_m^2}{2}}=\frac{E_m}{\sqrt{2}} \]

교류 순시전력

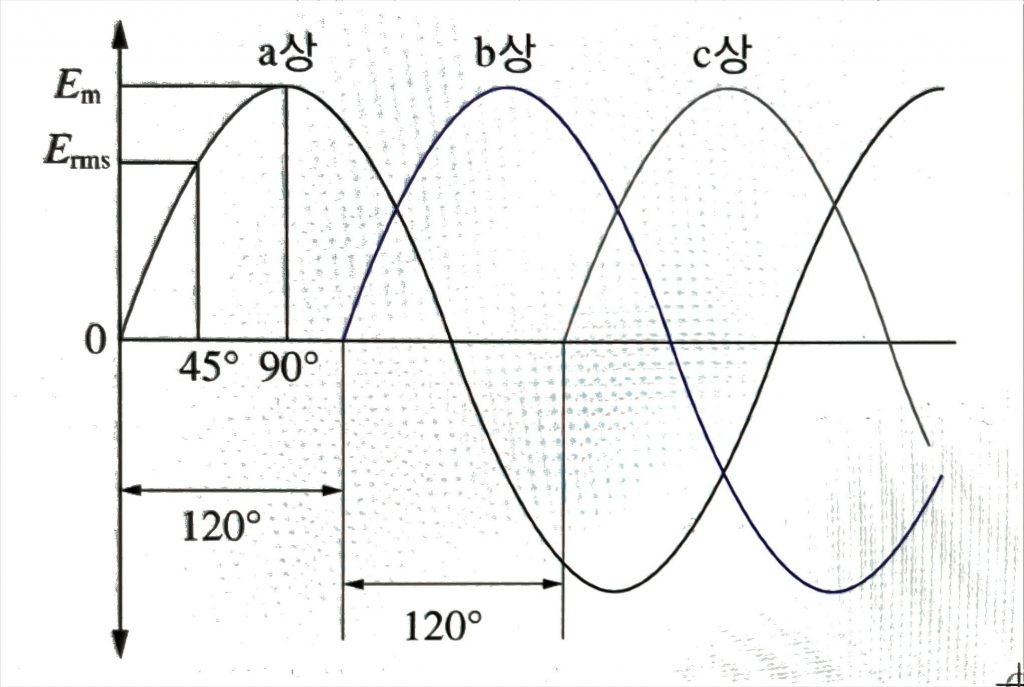
a상의 순시전력

\[ e_a=E_{am}\sin\omega t\]\[ i_a=\sin(\omega t-\theta) \]

–

\[ p_a=E_{am}I_{am}\sin\omega t\sin(\omega t-\theta)\]\[=2E_aI_a\sin\omega t\sin(\omega t- \theta)\] \[ =E_aI_a\cos\theta -E_aI_a\cos(2\omega t-\theta) \]

–

\[여기서/ E_aI_a\cos\theta : 일정한전력 \] \[E_aI_a\cos(2\omega t-\theta) : \]\[2배의\ 주파수로\ 변하는\ 전력 \]

b상 순시전력

\[ e_b=E_{bm}\sin\omega t-240\]\[ i_b=I_{bm}\sin(\omega t-240-\theta) \]

–

\[ p_b=E_{bm}I_{bm}\sin\omega t-240\sin(\omega t-240-\theta)\]\[=2E_bI_b\sin\omega t-240\sin(\omega t-240- \theta)\] \[ =E_bI_b\cos\theta -E_bI_b\cos(2\omega t-480-\theta) \]

c상 순시전력

\[ e_c=E_{cm}\sin\omega t-120\]\[ i_c=I_{cm}\sin(\omega t-120-\theta) \]

–

\[ p_c=E_{cm}I_{cm}\sin\omega t-120\sin(\omega t-120-\theta)\]\[=2E_cI_c\sin\omega t-120\sin(\omega t120- \theta)\] \[ =E_cI_c\cos\theta -E_cI_c\cos(2\omega t-240-\theta) \]

순시 전력의 합

\[ P_3=E_aI_a\cos\theta-E_aI_a\cos(2\omega t-\theta)\] \[ +E_bI_b\cos\theta-E_bI_b\cos(2\omega t-\theta-480)\] \[ +E_cI_c\cos\theta-E_cI_c\cos(2\omega t-\theta-240)\] \[=3EI\cos\theta\]