인덕턴스/3상 1회선 1선당 작용 인덕턴스/
정전용량/예제1/예제2/
특성 임피던스
특성 임피던스
(Characteristic Impedance)
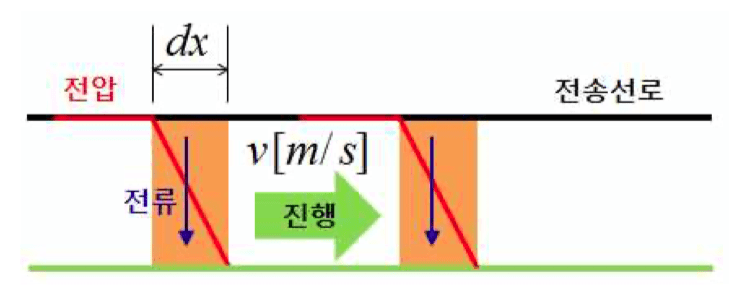
뇌서지, 개폐서지에 의해서 발생된 진행파 전압은 전송선로를 충전하면서 진행한다. 그때 진행파 전압이 선로를 충전하면서 충전전류가 순간적으로 흐르게 된다. 이 진행파 전압과 전류의 순시적인 비를 이 전송선로의 특성 임피던스라고 한다. 특성 임피던스가 다른 부분을 만나면 반사가 발생된다.
전송선로에서 파동임피던스의 해석은 무손실선로(r=0, G=0)인 조건으로 해석
\[Z_0=\sqrt{\frac{Z}{Y}}=\sqrt{\frac{r+jw}{g+jb}}\backsimeq\sqrt{\frac{j\omega L}{j\omega C}}=\sqrt{\frac{L}{C}}\]
전압, 전류의 진행파 개념으로 해석
dx구간에 충전될 전하량
\[dQ=CVdx\]
dx구간의 충전전류 (v : 진행파 전송속도)
\[I=\frac{dQ}{dt}=CV\frac{dx}{dt}=CVv\]
미소전류 Idx에의한 쇄교자속을 dΦ라 하면 인덕턴스는
\[I=\frac{d\Phi}{Idx}\to d\Phi=LI dx\]
유기기전력
\[V=\frac{d\Phi}{dt}=LI\frac{dx}{dt}=LIv\]
특성 임피던스
\[Z_0=\frac{V}{I}=\frac{LIv}{CVv}=\frac{LI}{CV}\]
\[\to Z_0=\sqrt{\frac{L}{C}}\to v=\frac{1}{\sqrt{LC}}\]
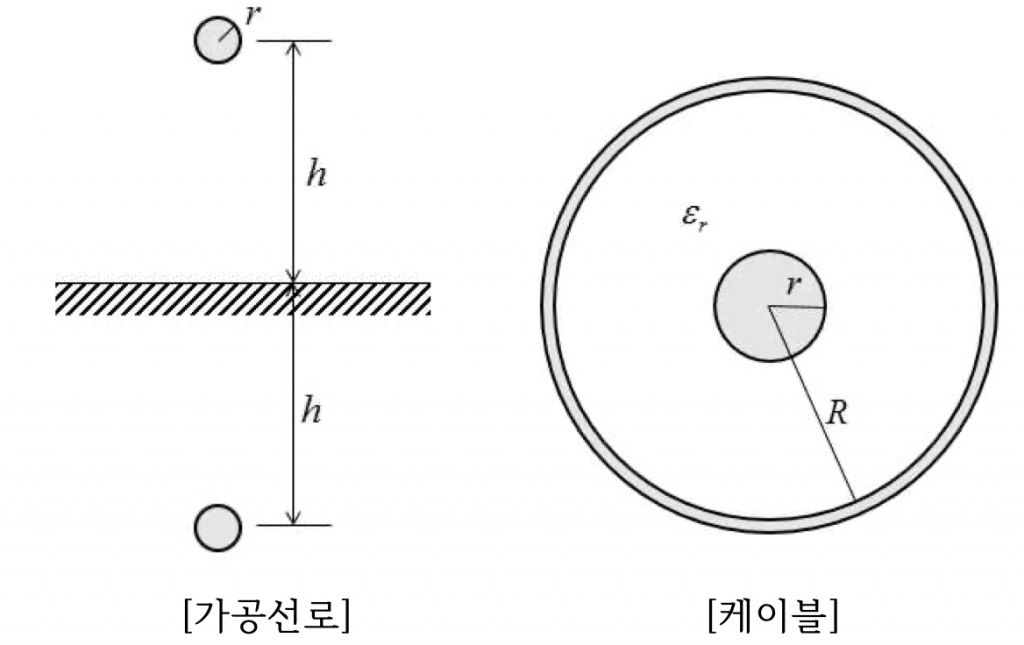
가공선로와 케이블의 특성 임피던스, 진행파 진행속도 비교
1) 인덕턴스
가공선
\[L\backsimeq 0.4605\log_{10}\frac{2h}{r}[mH/km]\]
케이블
\[L\backsimeq 0.4605\log_{10}\frac{R}{r}[mH/km]\]
2) 정전용량
가공선
\[C\backsimeq\frac{0.02413}{\log_{10}\frac{2h}{r}}[\mu F/km]\]
케이블
\[C\backsimeq\frac{0.02413\epsilon_r}{\log_{10}\frac{R}{r}}[\mu F/km]\]
3) 특성 임피던스
(가공선: 300~500[Ω], 케이블: 30~50[Ω])
가공선
\[Z_0=\sqrt{\frac{L}{C}}=\sqrt{\frac{0.4605\log_{10}\frac{2h}{r}\times 10^{-3}}{\frac{0.02413}{\log_{10}\frac{2h}{r}}\times 10^{-6}}}\]\[1.38\times \log{10}\frac{2h}{r}[\Omega]\]
케이블
\[Z_0=\sqrt{\frac{L}{C}}=\sqrt{\frac{0.4605\log_{10}\frac{R}{r}\times 10^{-3}}{\frac{0.02413\epsilon_r}{\log_{10}\frac{R}{r}}\times 10^{-6}}}\]\[\frac{138}{\sqrt{\epsilon_r}}\times \log{10}\frac{R}{r}[\Omega]\]
4) 진행파의 전파속도
(가공선: 광속, 케이블: 비유전률에 증가로 속도 감소)
① 가공선
\[v=1/\sqrt{LC}\]
\[=1/\sqrt{0.4605\log_{10}\frac{2h}{r}\times 10^{-3}\times \frac{0.02413}{\log_{10}\frac{2h}{r}}\times 10^{-6}}\]\[=3\times 10^8[m/s]\]
② 케이블
\[v=1/\sqrt{LC}\]
\[=1/\sqrt{0.4605\log_{10}\frac{R}{r}\times 10^{-3}\times \frac{0.02413\epsilon_r}{\log_{10}\frac{R}{r}}\times 10^{-6}}\]\[=\frac{3\times 10^8}{\sqrt{\epsilon_r}}[m/s]\]
답글 남기기