전기기초(소자) AB
V 전압, 전류 (AC1)
B 기준충격절연강도(BIL)
D 전압강하 (LMD)
S 변위전류 (AE)
F 패란티 현상 (QVF)
M 단락전자력 (LMMS)
이상전압 및 대책 (BS)
C 코로나 (AG)(LP)
코로나(임계전압식 유도⁕)
R 저항 임피던스 리액턴()
I 특성임피던스 ()
P 전력 역률
A 무효전력
L 최대전력전달
목차(유효전력과 무효전력 ABA)
무효전력과 유효전력
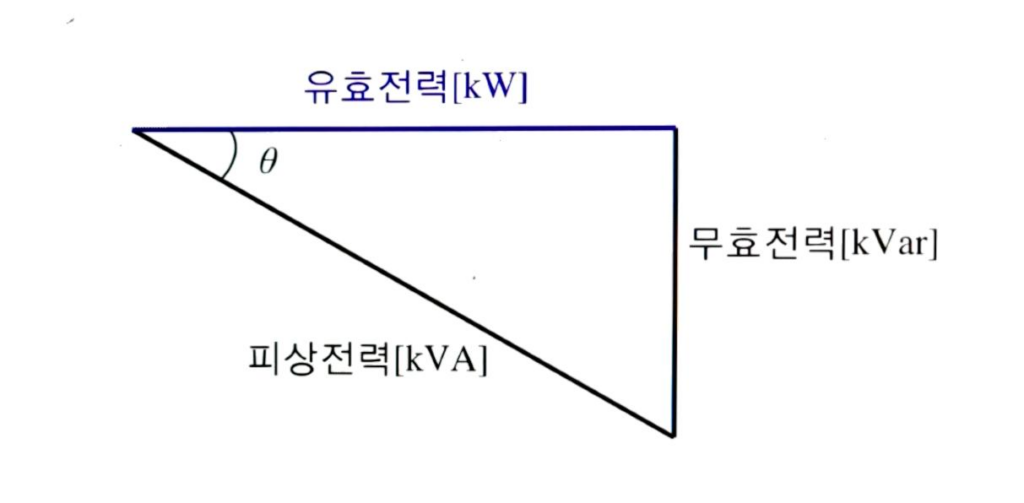
1️⃣유효전력
- 유효전력은 실제 일(Work)에 사용되는 전력 또는 저항과 같은 회로소자에 의해서 열로서 소비되는 전력
- 유효전력은 순시전력의 평균치 또는 유효분 순시전력의 평균치와 같음
\[P=\frac{1}{T}\int _0^Tp’\left(t\right)dt=\]
\[\frac{1}{T}\int _0^T\left\{VI\cos \theta \left(1-\cos 2\omega t\right)-VI\sin \theta \sin 2\omega t\right\}dt \]
\[=VI\cos \theta\]
\[P=VI\cos \theta \ \left[W\right]\]
2️⃣무효전력
- 무효전력은 실제로 아무 일도 하지 않고 열소비도 하지 않는 전력으로 인덕터 및 커패시터의 저장요소에서 에너지 저장과 방출을 반주기 마다 반복하는 전력
- 예를 들어, 모터나 변압기 등에서 발생
- 무효분 순시 전력의 평균치는 0이되므로 무효전력은 무효분 순시전력의 최대로 표시한다. 위의 결과에서 알수 있듯이 무효분 순시전력의 최대치는 VI sinθ 이다
\[Q=\frac{1}{T}\int _0^Tq\left(t\right)dt=0\]
무효전력은 평균치로 표현할수 없다
\[Q=VI\sin \theta \ \left[Var\right]\]
무효분 순시전력의 최대치를 사용
1)무효전력의 의의
- 유효전력 전달 매개:
- 무효전력은 유효전력이 부하까지 전달될 수 있도록 매개하는 역할
- 마치 물이 파이프를 통해 흐르기 위해서는 일정한 압력이 필요한 것처럼, 전력 시스템에서도 무효전력이 일정 수준 이상 유지되어야 유효전력이 안정적으로 전달될 수 있다.
- 전압 유지:
- 무효전력은 시스템의 전압을 유지하는 데 중요한 역할
- 무효전력이 부족하면 전압이 낮아지고, 과다하면 전압이 상승하게 됩니다. 따라서 적절한 무효전력 관리를 통해 안정적인 전압을 유지할 수 있습니다.
- 시스템 안정도 확보:
- 무효전력은 시스템의 안정도를 확보하는 데 기여
- 무효전력이 부족하거나 과다하면 시스템의 안정도가 저하되어 정전 등의 문제가 발생할 수 있습니다.
2)무효전력의 영향
- 전압 변동: 무효전력이 부족하면 전압이 저하되고, 과다하면 전압이 상승합니다. 전압 변동은 전력 설비의 수명을 단축시키고, 전력 품질을 저하시킬 수 있습니다.
- 전력 손실 증가: 무효전력이 증가하면 전력선에서의 손실이 증가하여 에너지 효율이 저하됩니다.
- 시스템 안정도 저하: 무효전력 불균형은 시스템의 안정도를 저하시켜 정전 등의 문제를 야기할 수 있습니다.
- 설비 용량 증가: 무효전력을 보상하기 위해 발전기 용량을 증가시켜야 할 수 있습니다.
3)무효전력과 전압
- 무효전력은 적절한 전압을 일정하게 유지하기 위한 전력
- 전압이 큰 쪽은 역률이 나빠지고, 작은쪽은 역률이 개선되어 적정전압을 유지
4)무효전력의 조정
- 무효전력의 소비가 늘면 송전과정에서 전압이 지나치게 낮아져 정전 발생
- 전력거래소에서는 전력계통의 안정과 효율적인 운영을 위해 조상설비 가동을 지시
- 무효전력량을 조절하는 보조 서비스운영
3)무효 전력의 종류
- 유도성 무효 전력: 모터 등의 유도성 부하에서 발생하는 무효 전력입니다.
- 용량성 무효 전력: 케이블, 콘덴서 등의 용량성 부하에서 발생하는 무효 전력입니다.
5)무효전력 보상
무효전력을 보상하기 위해서는 진상 콘덴서를 설치합니다. 진상 콘덴서는 유도성 부하에서 소비되는 무효전력을 보상하여 시스템의 역률을 개선시키는 역할을 합니다.
- 콘덴서: 용량성 무효 전력을 공급하여 유도성 무효 전력을 상쇄
- 동기 조상기: 유도성 또는 용량성 무효 전력을 공급하여 무효 전력을 조절
- 정지형 무효 전력 보상 장치 (SVC): 반도체 스위칭 소자를 이용하여 빠르고 정확하게 무효 전력을 조절
3️⃣부하에 공급되는 순시전력
부하에 인가된 전압이
\[v\left(t\right)=\sqrt{2}V\sin \omega t\ \left[V\right]\]
지상역률의 θ 인 부하에 전력을 공급한다.
이때 부하에 흐르는 전류는 다음과 같다,
\[i\left(t\right)=\sqrt{2}I\sin \left(\omega t-\theta \right)\ \left[A\right]\]
1)전압과 전류 페이저도 및 유효분과 무효분 전류
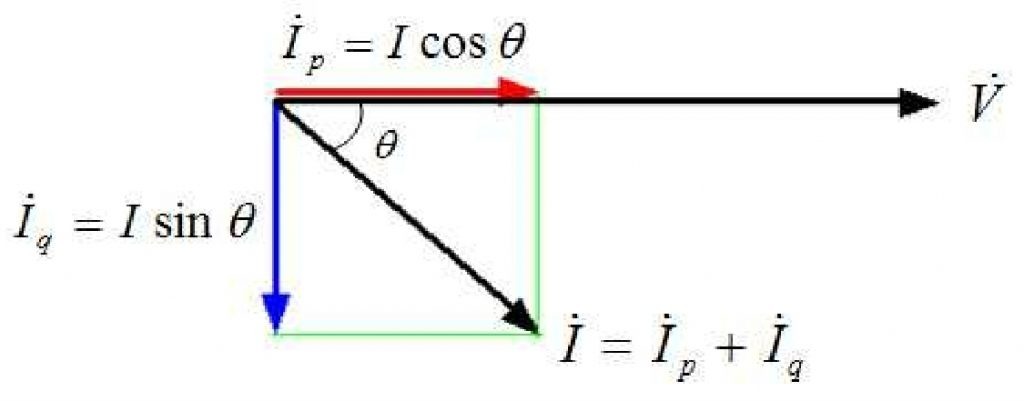
유효분전류
\[\ I_p=I\cos \theta \to 전압과\ 동상인\ 성분\]
무효분전류
\[\ I_q=I\sin \theta \to 전압과\ 90º 위상차\ 성분\]
2)유효분 순시전력 및 무효분 순시전력
(1)유효분 순시전력 : 전압의 순시치와 유효분 전류의 순시치의 곱

\[p\left(t\right)=v\left(t\right)\times i_p\left(t\right)\]
\[=\sqrt{2}V\sin \omega t\times \sqrt{2}I\cos \theta \sin \omega t\]
\[=VI\cos \theta -VI\cos \theta \cos 2\omega t\]
\[=VI\cos \theta \left(1-\cos 2\omega t\right)\]
(2)무효분 순시전력 : 전압의 순시치와 무효분 전류의 순시치의 곱
\[q\left(t\right)=v\left(t\right)\times i_q\left(t\right)\]
\[=\sqrt{2}V\sin \omega t\times \sqrt{2}I\sin \theta \sin \left(\omega t-\frac{\pi }{2}\right)\]
\[=-VI\sin \theta \sin 2\omega t\]
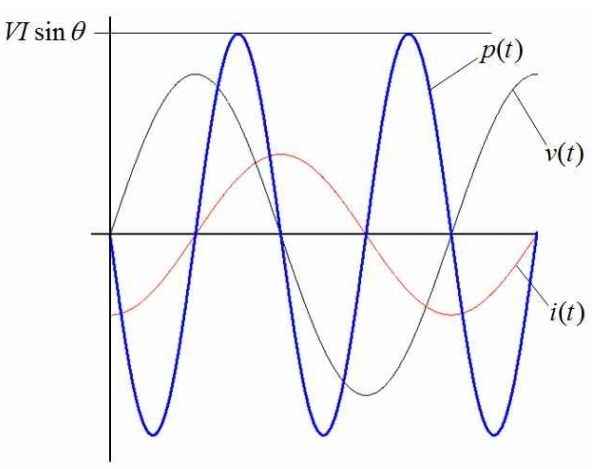
(3)순시전력
\[P\left(t\right)=v\left(t\right)\times i\left(t\right)=p\left(t\right)+q\left(t\right)\]
\[=VI\cos \theta \left(1-\cos 2\omega t\right)-VI\sin \theta \sin 2\omega t\]
전기기초(소자) AB
V 전압, 전류 (AC1)
B 기준충격절연강도(BIL)
D 전압강하 (LMD)
S 변위전류 (AE)
F 패란티 현상 (QVF)
M 단락전자력 (LMMS)
이상전압 및 대책 (BS)
C 코로나 (AG)(LP)
코로나(임계전압식 유도⁕)
R 저항 임피던스 리액턴()
I 특성임피던스 ()
P 전력 역률
A 무효전력
L 최대전력전달
목차(유효전력과 무효전력 ABA)
무효전력과 유효전력
🌐V1001P24
답글 남기기