폐열회수
B3절탄기효율
\[ m_f\times C_{pf}\times(T_{fi}-T_{fo})=m_a\times C_{pa}\times(T_{ai}-T_{ao}) \]
B3 폐열회수계산
\[Q_s=G_s\times C_s\times \Delta t \times \eta \]
보일러 연도에 설치된 절탄기의 조건이 [보기]와 같을 때 효율[%] 을 구하시오.
절탄기에서 가열된 급수량 : 40,000[kg/h]
배기가스량 : 50,000[kg/h]
절탄기 입구 급수온도 : 25[℃]
절탄기 출구 급수온도 : 55[℃]
절탄기 입구 배기가스 온도 : 350[℃]
절탄기 출구 배기가스 온도 : 230[℃]
급수의 비열 : 4.185[kJ/kg·℃]
배기가스 비열 : 1.05[kJ/kg·℃]
$$ Q_w=Q_f\times \eta $$
$$ m_w\times C_w\times \Delta t_w=G_f\times C_f\times\Delta t_f\times \eta $$
$$ 4.185\times40000\times(55-25) = \\ 1.05\times50000\times(350-230)\times\eta $$
$$\eta=\frac{4.185\times40000\times(55-25)}{1.05\times50000\times(350-230)}=0.7971 $$
벙커C유를 사용하는 보일러에서 급수온도를 65[℃]에서 80[℃]로 상승시켰을 때 연료절감률[%]은 얼마인가?
(단, 발생증기 엔탈피는 639[kcal/kg]이고. 보일러 효율은 변함이 없다.)
$$ Q_s=G_s\times C_s\times \Delta t \times \eta $$
$$ \Delta Q=\frac{(639-65)-(639-80)}{639-65}\times100=2.61[\%] $$
시간당 50,000[kg]의 물을 절탄기를 통해 60[℃]에서 90[℃]로 높여 보일러에 급수한다. 절탄기 입구 배기가스 온도가 340[℃]이면 출구온도는 몇 [℃]인가?
(단, 배기가스량은 75,000[Nm³/h], 배기가스 비열 1.05[kJ/Nm³·℃] 급수 비열 4.2[kJ/kg·℃], 절탄기 효율은 80[%]이다)
B3절탄기효율
\[ m_f\times C_{pf}\times(T_{fi}-T_{fo})=m_a\times C_{pa}\times(T_{ai}-T_{ao}) \]
절탄기에서 물이 흡수한 열량은 배기가스가 전달해준 열향의80%에 해당한다
\[Q_1=Q_2\times \eta\]
\[G_w\times C_w\times\Delta t_w=G_f\times C_f\times \Delta t_f\times \eta \]
\[\Delta t_f=\frac{G_w\times C_w\times\Delta t_w}{G_f\times C_f\times \eta}\]
\[t_{f1}=t_{f2}-\frac{G_w\times C_w\times\Delta t_w}{G_f\times C_f\times \eta}\]
\[=340-\frac{50000\times 4.2\times(90-60)}{75000\times 1.05 \times \times 0.8}=240\]
열효율
동작물질 1[kg]이 고열원 600[°C], 저열원 100[°C]사이에서 분당 60사이클(cycle)로 회전하는 카르노 사이클 기관의 최고압력(P₃)이 400[kPa·a]이고, 등온팽창하여 압력(P₄)이 200[kPa·a]로 되었다면 1시간 동안에 수열되는 열량[kW]은 얼마인가? (단, 동작물질의 기체상수 R=287[J/kg·K]이다)
N1 카르노사이클
$$ \eta=\frac{W}{Q_1}=1-\frac{Q_2}{Q_1}=1-\frac{T_2}{T_1} $$
$$ \Delta S_1=\frac{Q_1}{T_1}(엔트로피) $$
$$ W_2=Q_2=\frac{T_2}{T_1}\times Q_1 $$
$$ Q_1=m\times P_3 \times v_3\times\ln\frac{v_3}{v_4}=m\times R \times T_H\times \ln\frac{P_3}{P_4} $$
시간당 사이클수=60사이클/분*60분=3600사이클/시
$$\eta=1-\frac{T_c}{T_h}=1-\frac{373.15}{873.15}=0.573$$
등온팽창과정중 일과 열교환량 계산
$$ Q_1=m\times P_3 \times v_3\ln\frac{v_3}{v_4}=m\times R \times T_H\times \ln\frac{P_3}{P_4} $$
$$ =1\times 0.287 \times (273+600)\ln\frac{400}{200}=173.668[kJ] $$
$$ 수열량=\frac{173.67\times 60\times 60}{3600}=173.67[kW] $$
1시간 동안 수열되는 총 열량(kW)
$$ 수열량=\frac{1사이클당 수열량\times 1분당사이클수\times 60}{3600[kJ/h]} \\ =\frac{173.67\times60\times60}{3600}=173.67[kW] $$
온도가 600[K]인 고온열원과 400[K]인 저온열원 사이에서 작동하는 카르노사이클에서 단열압축과정의 엔트로피 변화량이 100[J/K]으로 일정할 때 다음 물음에 답하시오.
(1) 공급받은 열량[J]은 얼마인가?
N1 카르노사이클
$$ \eta=\frac{W}{Q_1}=1-\frac{Q_2}{Q_1}=1-\frac{T_2}{T_1} $$
$$ \Delta S_1=\frac{Q_1}{T_1}(엔트로피) $$
$$ W_2=Q_2=\frac{T_2}{T_1}\times Q_1 $$
$$ Q_1=m\times P_3 \times v_3\times\ln\frac{v_3}{v_4}=m\times R \times T_H\times \ln\frac{P_3}{P_4} $$
1)
$$ \Delta S_1=\frac{Q_1}{T_1} $$
$$ Q_1=T_1\times\Delta S_1=600\times 100=60,000[J] $$
2)
$$ \eta=\frac{W}{Q_1}=1-\frac{Q_2}{Q_1}=1-\frac{T_2}{T_1} $$
$$ (1-\eta)=\frac{Q_2}{Q_1}=\frac{T_2}{T_1} $$
$$ Q_2=Q_1\times\frac{T_2}{T_1}=T_2\times\frac{Q_1}{T_1}=T_2\times\Delta S_1 $$
$$ Q_2=T_2\times\Delta S_1=400\times 100=40000[J] $$
$$ W=Q_1-Q_2=60000-40000=20000[J] $$
3)
$$ \Delta S_2=\frac{Q_2}{T_2}=\frac{40000}{400}=100[J/K] $$
4)
$$ \eta=\frac{W}{Q_1}\times 100=\frac{20000}{60000}\times 100=33.33 $$
정압비열이 20.9[kJ/kmol・K]인 이상기체를 25[°C], 1[atm] 상태에서 가역단열과정으로 10[atm]까지 압축하였을 때 온도는 몇 [°C]인가? (단, 0[K]는 -273.15[°C]를 기준으로 한다.)
● 정적비열 계산 기체상수 R=8.314[kJ /kmol・K]이다.
$$ C_v=C_p-R=20.9-8.314=12.546[kJ/kmol K] $$
● 비열비계산
$$ k=\frac{C_p}{C_v}=\frac{20.9}{12.59}=1.66 $$
● 압축후 온도계산
$$ \frac{T_2}{T_1}=(\frac{P_2}{P_1})^{\frac{k-1}{k}} $$
$$ T_2=T_1\times(\frac{P_2}{P_1})^{\frac{k-1}{k}}=(273+25)\times(\frac{10}{1})^{\frac{1.66-1}{1.66}}=744.400[K]-273=471.4[℃] $$
N0 단열압축
$$ \frac{T_2}{T_1}=(\frac{P_2}{P_1})^{\frac{k-1}{k}} $$
$$ T_2=T_1\times(\frac{P_2}{P_1})^{\frac{k-1}{k}}=(273+25)\times(\frac{10}{1})^{\frac{1.4-1}{1.4}} \\ =575.347[K]-273=302.347[℃] $$
✋ N7 폴리트로픽 9️⃣ 19A정적비열 Cv=0.72[kJ/kg·K]인 산소 10[kg]이 350[℃]에서 “PV1.3=일정”인 폴리트로픽 변화 에 따라 압축일 90,000[kgf·m]하였을 때 엔트로피 변화는 몇[kJ/K]인가. (단, 산소의 기체상수는 26.5[kgf·m/kg·K]이다)
● 정압비열계산
$$ C_p-C_v=R \\ R=\frac{8.314}{M}[kJ/kg\cdot K] $$
$$ C_p=C_v+R=0.72+\frac{8.314}{32}=0.979[kJ/kg\cdot K] $$
● 산소의 비열비 계산
$$ k=\frac{C_p}{C_v}=\frac{0.98}{0.72}=1.361 $$
● 압축후 온도 계산
$$ W_t=\frac{n}{n-1}GR(T_2-T_1) \\ (T_2-T_1)=\frac{W_t}{\frac{n}{n-1}GR}$$
$$ T_2=T_1-\frac{W_t}{\frac{n}{n-1}GR} \\ =(350+273)-\frac{90000}{\frac{1.3}{1.3-1}\times10\times26.5}=544.625$$
● 엔트로피 변화 계산
$$ \Delta S=mC_n\ln\frac{T_2}{T_1}=10\times0.72(\frac{1.3-1.36}{1.3-1})\ln\frac{544.63}{360+273}=0.193[kJ/K]$$
압력이 0.1[MPa], 온도가 27[℃]인 증기 1[kg]이 PVn=C(일정)이고 n=1.3인 폴리트로픽 변화를 거쳐 300[°C]가 되었을 때 엔트로피[kcal/K] 변화를 계산하시오 (단, 비열비 k = 1.4. 정적비열 Cv=0.17[kcal/kg·K], 압력은 절대압력이다.)
$$ \frac{T_2}{T_1}=(\frac{V_1}{V_2})^{n-1}=(\frac{P_2}{P_1})^{\frac{n-1}{n}} $$
$$ \frac{T_2}{T_1}=\frac{273+300}{273+27}=1.91 $$
$$ (\frac{P_2}{P_1})^{\frac{n-1}{n}}=(\frac{P_2}{P_1})^{\frac{1.3-1}{1.3}}=(\frac{P_2}{P_1})^{0.230} $$
$$ 1.91=(\frac{P_2}{P_1})^{0.230} \\ \frac{P_2}{P_1}=^{0.230}\sqrt{1.91} $$
$$P_2=P_1\times^{0.230}\sqrt{1.91}=1.67[MPa] $$
실린더 내에 있는 이상기체 10[kg]을 350[°C]상태에서 폴리트로픽 과정으로 압축하는 일량이 900[kJ]이 소요되었을 때 엔트로피 변화량[kJ/K]을 계산하시오. (단, 정적비열은 0.72[kJ/kg・K], 기체상수 0.26[kJ/kg・K] 폴리트로픽 지수 1.3, 비열비 1.4이다)
$$ W_a=m\times \frac{R}{n-1}\times(T_1-T_2) $$
$$ T_2=T_1-\frac{W}{m-\frac{R}{n-1}} \\ =(273+350)-\frac{900}{10\times \frac{0.26}{1.3-1}}=519.153[K] $$
$$ \Delta s=m\times C_v\times \frac{n-k}{n-1}\times \ln\frac{T_2}{T_1} $$
$$ =10\times 0.72\times \frac{1.3-1.4}{1.3-1}\times \ln\frac{519.15}{273+350}=0.437[kJ/K] $$
2️⃣랭킨사이클 18A11 18C
랭킨사이클로 작동하는 증기원동소에서
N4 랭킨사이클(효율)
\[ \eta=\frac{W_T}{Q_1}\times 100=\frac{h_3-h_4}{h_3-h_2}\times 100 \]
\[ =\frac{3465-2556}{3465-135}\times100=27.297[\%] \]
랭킨 사이클로 작동하는 증기원동소에서 터빈입구에서 엔탈피가 843.3[kcaI/kg], 터빈출구에서 엔탈피가 493.3[kcaI/kg]인 증기를 이용하여 500,000[kWh]의 전력을 발생하는데 필요한 증기량[ton]을 계산하시오
$$ m\times(h_2-h_3)=860\times 전열량 $$
$$ m=\frac{860\times 전열량}{h_3-h_4} $$
$$ =\frac{860\times 500,000}{843.3-493.3}=1,228.57[ton] $$
랭킨 사이클에 의한 증기 원동소에서 2.47[MPa], 220[°C]의 과열증기 50[kPa]까지 터빈에서 단열 팽창시킬 때 다음 증기표를 이용하여 **터빈의 출력[kW]**을 계산하시오. (단, 터빈 출구의 증기 건도는 0.93, 공급되는 증기는 20[ton/h], 압력은 절대압력이다.)
절대압력 포화수 엔탈피 건포화증기 엔탈피 0.05 338.19 2642.41 2.47 963.05 2800.18
● 터빈 입구의 증기엔탈피 h3 : 2800.18
● 터빈출구의 증기 엔탈피 계산
$$ h_4=h’+(h”-h’)\times x \\338.19+(2642.41-338.19)\times 0.93 \\ =2481.114[kJ/kg] $$
● 터빈 출력 계산
$$ 1[kW]=1[kJ/s]=3600[kcal/h] \\ N_T=\frac{m(h_3-h_4)}{3600}$$
$$=\frac{(20\times10^3)\times (2800.18-2481.11)}{3600}=1772.611[kW] $$
1️⃣7️⃣N4 랭킨사이클 22C
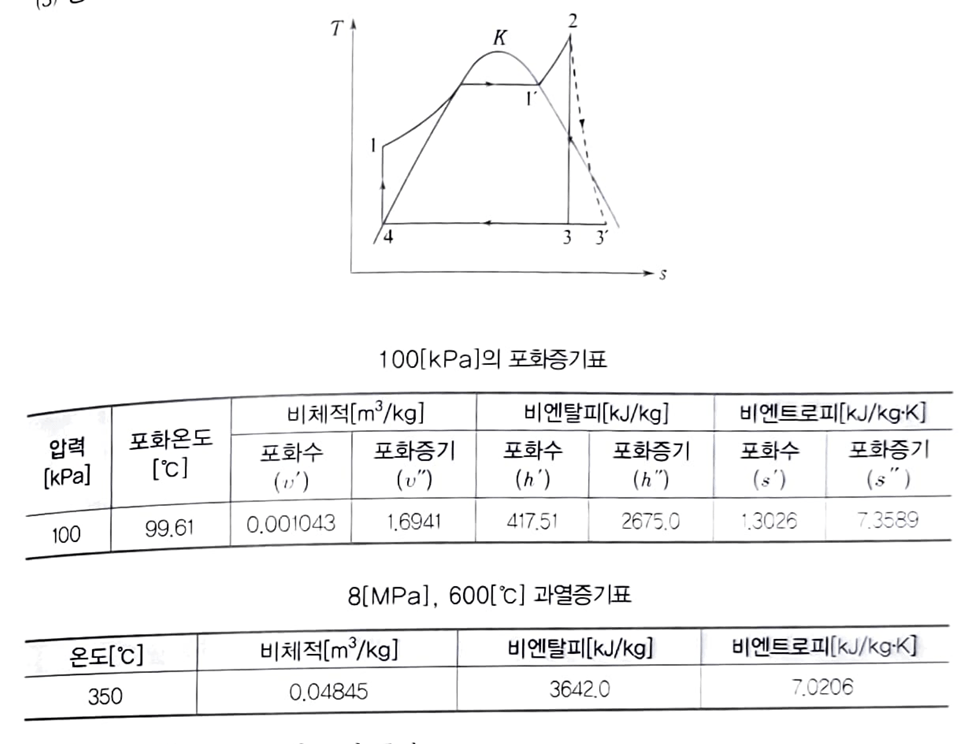
랭킨 사이클에서 최고압력 8[MPa], 최고온도 600[℃],
(단, 랭킨사이클 선도에서 2-3’구간은 열손실이 발생하였고 나머지 구간은 이론 변화가 정상적으로 이루어 졌다.)
(1) 복수기 입구의 실제 엔탈피(h3)를 구하시오.
(2) 보일러 입구의 엔탈피(h1)를 구하시오. (단 펌프 압축률은 무시한다)
(3) 랭킨 사이클 효율을 구하시오.
복수기 입구의 건조도 계산 터빈이 팽창과정은 등엔트로피과정이므로 s2=s3이고 s2=s3’+x3(s3’’-s3’)에서 건조도 x3를 구한다
$$ x_3=\frac{s_2-s_3′}{s_3”-s_3′}=\frac{7.0206-1.3026}{7.3589-1.3026}=0.9441 $$
1)복수기 입구(터빈출구)의 비엔탈피(h3)계산
$$ h_3=h_3’+x_3(h_3”-h_3′) \\ =417.51+0.9441*(2675.0-417.51) \\ =2548.806[kJ/kg] $$
2)복수기 입구(터빈출구)의 실제 엔탈피계산 : 터빈의 열효율
$$ \eta_T=\frac{실제터빈일}{이론터빈일}=\frac{h_2-h_3′}{h_2-h_3} $$
$$ h_3’=h_2-\eta_T(h_2-h_3) \\ =3642.0-0.9(3642.0-2548.81)=2658.129[kJ/kg] $$
$$ W_P=h_1-h_4=v’_4(P_2-P_1) $$
$$ h_1=h_4+v_4(P_2-P_1) \\ =417.51+0.001043*((8*1000)-100)=425.749[kJ/kg] $$
3)펌프일을 감안한 이론 열효율 계산
$$ \eta_R=\frac{(h_2-h_3)-(h_1-h_4)}{h_2-h_1}\times 100 \\ \frac{(3642.0-2548.81)-(425.75-417.51)}{3642.0-425.75}\times100=33.733[\%] $$
1️⃣7️⃣N4랭킨사이클 18
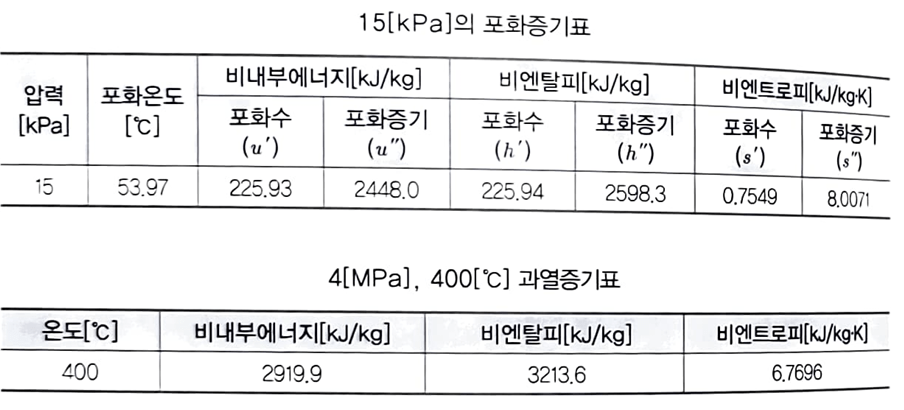
랭킨 사이클로 작동되는 터빈에 4[MPa] 400[℃] 과열증기가 2[kg/s]로 공급되어 터빈에서 등엔트로피 팽창한 후 15[kPa]이 되었다. 다음 표를 이용하여 물음에 답하시오. (단, 터빈에서 실제로 발생되는 동력은 1.5[MW]이고, 펌프의 소요동력은 무시한다)
(1)터빈 출구의 건조도를 구하시오
(2)터빈의 효율[%]을 구하시오
● 건조도(비엔트로피)
$$ x_3=\frac{s_2-s_3′}{s_3”-s_3′} $$
$$ =\frac{6.7696-0.7549}{8.0071-0.7549}=0.829 $$
● 비엔탈피
$$ h_3=h_3’+x_3\times(h_3”-h_3′) $$
$$ =225.94+0.83\times(2598.3-225.94)=2194.998 $$
● 터빈출력
$$ W_T=m\times(h_2-h_3) $$
$$ W_T=2\times(3213.6-2195)=2037.2 $$
$$ \eta=\frac{1500}{2037.2}\times100=73.64[\%] $$
✋ 6️⃣ 간극체적이 행정체적의 15[%]인 오토사이클의 이론 열효율은 얼마인가? (단, 비열비는 1.4이다.)
압축비 계산
이론열효율계산
보일러효율
6️⃣보일러효율 16A HL 18A 18C
보일러의 운전 조건이 [보기]와 같을때 물음에 답하시오.
급수사용량 : 4000[L/h]
B-C유 소비량 : 300[L/h]
급수온도 : 90[℃]
포화증기 엔탈피 : 673.5[kcal/ kg ]
연료 발열량 : 9800[kcal/kg]
급수 비체적 : 0.001036[㎥/kg]
급유온도 : 65 [℃]
15[℃]의 B-C유 비중 : 0.965
온도에 따른 체적 보정계수(k) : 0.9754- 0.00067(t-50)
(1) 시간당 증기 발생랑[kg]을 구하시오.
C4 보일러효율
$$ \eta=\frac{G_a\times (h_2-h_1)}{G_f\times H_l}\times 100 $$
$$ \eta=(1-\frac{손실열}{입열})\times 100 $$
시간당 증기발생량
$$ G_a=\frac{급수량[m^3/h]}{비체적[m^3/kg]} $$
$$ =\frac{4000\times10^{-3}}{0.001036}=3861.00[kg/h] $$
시간당 연료소비량
$$ G_f=d\times k\times V_t $$
$$ 0.965\times\{0.9754-0.00067*(65-50)\}*300=279.468=279.47[kg/h] $$
보일러효율
$$ \eta=\frac{G_a\times (h_2-h_1)}{G_f\times H_L}\times 100 $$
$$ =\frac{3862\times (673.5-65)}{279.47\times9800}\times 100=82.258=82.26[\%] $$
[보기]와 같은 조건으로 운전되는 보일러에 대한 물음에 답하시오.
증기발생량 : 1200[kg/h]
보일러 압력 : 400[kPa]
연료 소비량 : 10.5[N㎥/min]
연료의 저위발열량 : 5800[kJ/Nm]
연료 공급압력 : 40[kPa]
연료의 공급온도 : 10[℃]
발생증기 엔탈피 : 2796[kJ/kg]
급수 엔탈피 : 49[kJ/kg]
C4 보일러효율
$$ \eta=\frac{G_a\times (h_2-h_1)}{G_f\times H_l}\times 100 $$
$$ \eta=(1-\frac{손실열}{입열})\times 100 $$
(1) 연료의 발열량[kJ/㎥]을 구하시오.
\[V_1=\frac{P_0\times V_0\times T_1}{P_1 \times T_0} \]
\[ =\frac{101.325\times 1\times (273+10)}{(101.325+40) \times 273}=0.743[m^3] \]
\[H’=H_l\times V_1=5800\times \frac{1}{0.74}=7837.837[kJ/m^3] \]
(2) 보일러 효율[%]을 구하시오.
\[\eta=\frac{G_a\times (h_2-h_1)}{G_f\times H_l}\times 100 \]
\[=\frac{1200\times (2796-49)}{(10.5\times 60)\times 7837.84}\times 100 \]
보일러효율16B16
습포화증기의 엔탈피를 구하시오
상당증발량을 계산하시오
전열면의 상당증발량을 구하시오
보일러의 효율을 계산하시오
[보기]의 조건으로 운전되는 보일러의 효율[%]을 계산하시오.
연료의 연소열 : 1200[MJ/kg] 배기가스 손실열 : 80[MJ/kg] 미연소분에 의한 손실열 : 40[MJ/kg]
C4 보일러효율
$$ \eta=\frac{G_a\times (h_2-h_1)}{G_f\times H_l}\times 100 $$
$$ \eta=(1-\frac{손실열}{입열})\times 100 $$
$$ \eta=(1-\frac{손실열}{입열})\times 100 $$
$$ =(1-\frac{80+40}{1200})\times 100=90[\%] $$
중유를 110[kg/h] 연소시키는 보일러가 있다. 이 보일러의 증기압력이 1[MPa], 급수온도가 50[°C], 실제 증발랑이 1500 [kg/h]일 때 보일러의 효율[%]을 구하시오.
(단, 중유의 저위발열량은 40,950[kJ/kg]이며, 1[MPa]하에서 증기엔탈피는 2,864[kJ/kg], 50[°C] 급수엔탈피는 210[kJ/kg]이다.)
C4 보일러효율
$$ \eta=\frac{G_a\times (h_2-h_1)}{G_f\times H_l}\times 100 $$
$$ \eta=(1-\frac{손실열}{입열})\times 100 $$
$$ \eta=\frac{G_a\times(h_2-h_1)}{G_f\times H_l}\times 100 $$
$$ =\frac{1500\times(2864-210)}{110\times 40950}\times 100 =88.378[\%] $$
보일러로부터 압력 2[MPa]로 공급되는 수증기의 건도가 0.8일 때 이 습증기의 엔탈피[kJ]는 얼마인가? (단, 2[MPa]에서 포화수엔탈피는 1,000[kJ/kg], 포화증기엔탈피는 3,000[kJ/kg]이다.)
$$ h_2=h’+(h”-h’)\times x $$
$$ =1000+(3000-1000)\times 0.8=2600[kJ] $$
👍 1️⃣6️⃣보일러 계산
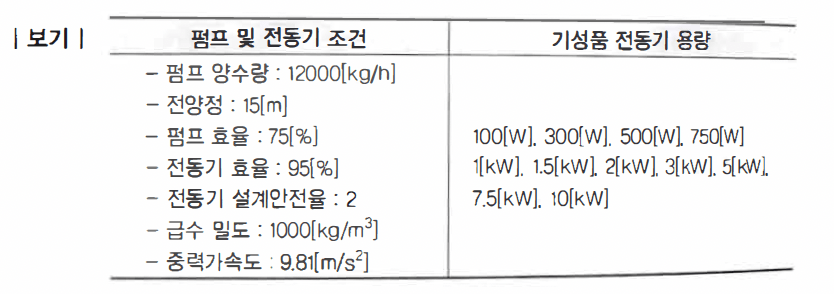
보일러 급수펌프의 전동기(motor)에 고장이 발생하여 교체하고자 한다. [보기]의 펌프 및 전동기 조건을 이용하여 물음에 답하시오
(1)교체할 전동기 용량을 계산하시오
(2)계산된 전동기 용량으로 보기에 제시된 기성품 전동기 중에서 최소 용량의 것을 선택하시오
C3 보일러 용량계산
\[ kW=\frac{P\times Q}{\eta_p}=\frac{(\gamma \times H)\times Q}{\eta_p}=\frac{(\rho\times g\times H)}{\eta_p} \]
$$ =\frac{(1000\times 9.81\times 15)\times(\frac{12000}{1000\times 3600})}{0.75}=654[W] $$
$$ 전동기용량=\frac{펌프축동력\times \alpha}{\eta_m}=\frac{0.65\times 2}{0.95}=1.368 $$


답글 남기기