Table of Contents
🔯N 관련사이클
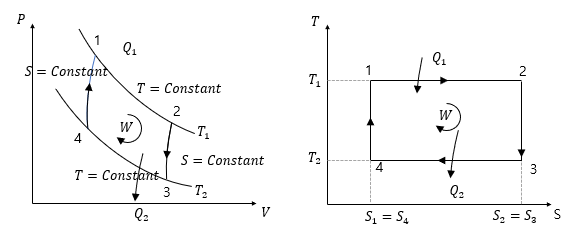
✋N1 카르노사이클
등온팽창->단열팽창->등온압축->단열압축
20A14►동작물질 1[kg]이 고열원 600[°C], 저열원 100[°C]사이에서 분당 60사이클(cycle)로 회전하는 카르노 사이클 기관의 최고압력(P₃)이 400[kPa·a]이고, 등온팽창하여 압력(P₄)이 200[kPa·a]로 되었다면 1시간 동안에 수열되는 열량[kW]은 얼마인가? (단, 동작물질의 기체상수 R=287[J/kg·K]이다)
- 카르노 사이클을 구성하는 과정 : 등온팽창→단열팽창→등온압축→단열압축
N1 카르노사이클
✋N2 증기 원동소 사이클
| 랭킨N4 (증기량) | 17C14 | 18C12 | ||
| 효율 | 23C17 | 22C12 | 18A11 | 18C16 |
| 25A18 | ||||
| 출력 | 24A18 | 19C15 | ||
| 건도 | 22A17 | |||
| 습증기 N5 | 20C14 | |||
| 재생재열 | 16C08 | 18C17 | ||
| 폴리N5 | 19A14 | 21C01 | ||
| 엔트로피 N7 | 16B15 | 17C13 | 20B15 | |
| 냉매순환 | 22C10 | |||
| 단열압축 |
랭킨사이클
단열등압
N4 랭킨사이클(효율)
17C14►랭킨 사이클로 작동하는 증기원동소에서
터빈입구에서 엔탈피가 843.3[kcaI/kg],
터빈출구에서 엔탈피가 493.3[kcaI/kg]인
증기를 이용하여 500,000[kWh]의 전력을 발생하는데
필요한 증기량[ton]을 계산하시오
N2 발전소 열효율공식
18C12►다음 그림은 랭킨사이클의 온도-엔트로피 선도이다 h₁=192[kJ/kg], h₂=194[kJ/kg], h₃=2802[kJ/kg], h₄=2010[kJ/kg] 일때, 열효율[%]을 구하시오.
23C17►랭킨사이클에서 포화수엔탈피 192.5[kJ/kg]과열증기 엔탈피 3002.5[kJ/kg], 습증기 엔탈피 2361.8[kJ/kg]일때 열효율%를 구하시오
(단 펌프의 동력은 무시한다)
18A11►랭킨사이클로 작동하는 증기원동소에서
터빈 입구의 과열증기 온도는 500[℃], 압력은 2[MPa]이며, 터빈 출구의 압력은 5[kPa]이다. 펌프일을 무시하는 경우 이 사이클의 열효율[%]을 계산하시오.
(단. 터빈 입구의 과열증기 엔탈피는 3,465[kJ/kg]이고, 터빈 출구의 엔탈피는 2,556[kJ/kg]이며, 5[kPa]일 때 급수엔탈피는 135[kJ/kg]이다.)
18C16►랭킨 사이클로 작동하는 증기원동소에서 과열증기 엔탈피 660[kcaI/kg], 습증기 엔탈피 530[kcal/kg], 포화수 엔탈피 80.87[kcal/kg]일 때 열효율[%]을 계산하시오.
25A18►랭킨 사이클에서 터빈 출구의 엔탈피 2210[kJ/kg]이고 보일러 출구 엔탈피는 2763[kJ/kg]이다. 펌프의 입구 엔탈피는 339[kJ/kg]라고 할 때 랭킨 열효율을 계산하시오(단, 펌프의 일은 무시한다)
19C15►랭킨 사이클에 의한 증기 원동소에서
2.47[MPa], 220[°C]의 과열증기 50[kPa]까지 터빈에서 단열 팽창시킬 때 다음 증기표를 이용하여
터빈의 출력[kW]을 계산하시오.
(단, 터빈 출구의 증기 건도는 0.93, 공급되는 증기는 20[ton/h], 압력은 절대압력이다.)
엔탈피
(증기 사이클 또는 베이퍼 사이클)
단열압축→정압가열→단열팽창→정압냉각
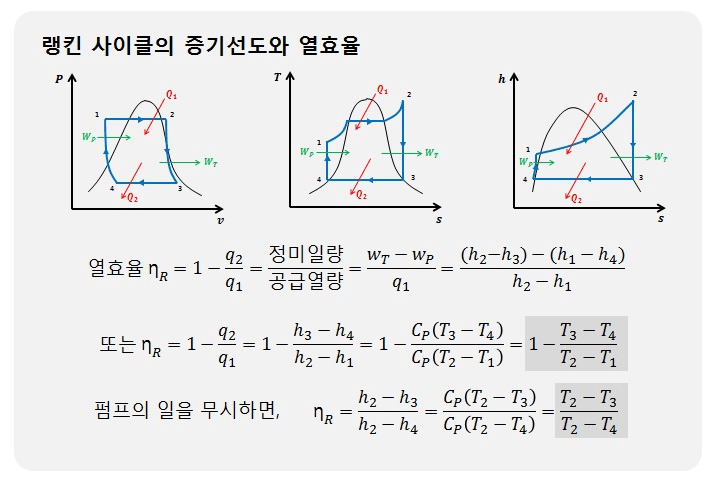
- 랭킨 사이클의 열효율
랭킨사이클의 열효율 향상요인
- 고대 : 초온, 초압, 보일러 압력, 고온측과 저온측의 온도차, 사이클 최고온도, 과열도(증기가 고온으로과열될수록 출력 증가)
- 저소 : 응축기(복수기)의 압역(배압)과 온도
- 재열기를 사용한 재열 사이클(2유체 사이클)에 의한 운전
응축기의 압력을 낮출 때 나타나는 현상
- 고대 : 이론 열효율이 향상된다
- 저소 : 터빈출구의 증기건도, 응축기의 포화온도, 응축기 내의 절대압력, 배출열량
랭킨사이클의 특징
- 랭킨사이틀에도 단점이 존재한다
- 카르노 사이클에 가깝다
- 포화수증기를 생산하는 핵동력장치에 가깝다.
22A18►랭킨 사이클로 작동되는 터빈에 4[MPa] 400[℃] 과열증기가 2[kg/s]로 공급되어 터빈에서 등엔트로피 팽창한 후 15[kPa]이 되었다. 다음 표를 이용하여 물음에 답하시오. 22A 22C
(단, 터빈에서 실제로 발생되는 동력은 1.5[MW]이고, 펌프의 소요동력은 무시한다)
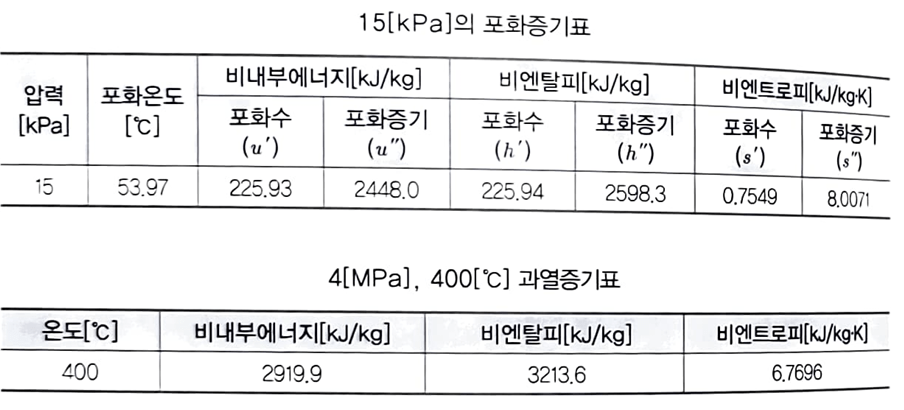
(1)터빈 출구의 건조도를 구하시오
(2)터빈의 효율[%]을 구하시오
● 건조도(x3) (비엔트로피)
● 비엔탈피(h3)
● 터빈 출력 계산
20C14►보일러로부터 압력 2[MPa]로 공급되는 수증기의 건도가 0.8일 때 이 습증기의 엔탈피[kJ]는 얼마인가? (단, 2[MPa]에서 포화수엔탈피는 1,000[kJ/kg], 포화증기엔탈피는 3,000[kJ/kg]이다.)
랭킨사이클로 작동하는 증기원동소에서
터빈 입구의 과열증기 온도는 500[℃], 압력은 2[MPa]이며, 터빈 출구의 압력은 5[kPa]이다. 펌프일을 무시하는 경우 이 사이클의 열효율[%]을 계산하시오.
(단. 터빈 입구의 과열증기 엔탈피는 3465[kJ/kg]이고, 터빈 출구의 엔탈피는 2556[kJ/kg]이며, 5[kPa]일 때 급수엔탈피는 135[kJ/kg]이다.)
N4 랭킨사이클(효율)
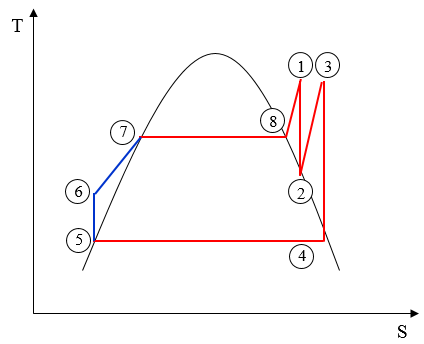
재열사이클
재생사이클
N6 재생사이클 재열사이클
● 재열사이클 : 증기의 초압을 높이면서 팽창후의 증기 건조도가 낮아지지 않도록한 것으로 효율증대보다는 터빈의 복수장해를 방지하여 수명연장에 주안점을 둔 사이클
● 재생사이클 : 팽창 도중의 증기를 터빈에서 추출하여 급수의 가열에 사용하는 사이클로 열효율이 랭킨 사이클에 비해 증가한다
N3가스동력 사이클
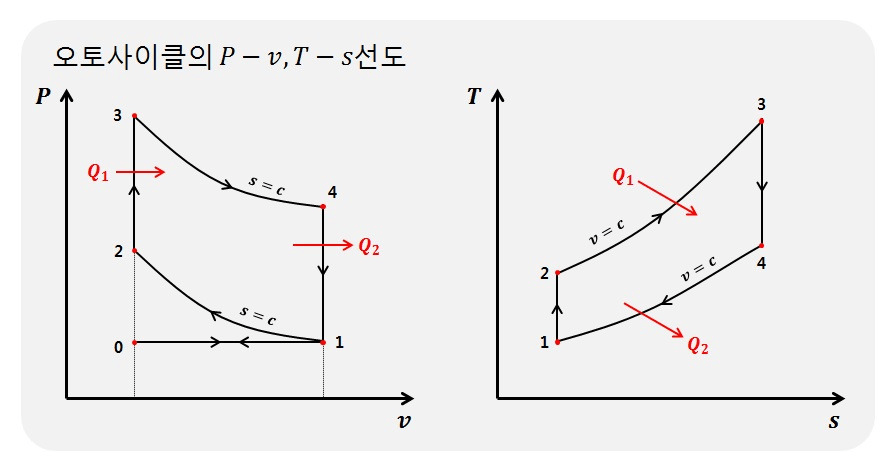
오토사이클
단열정적
적용 : 가솔린기관의 기본 사이클
구성 : 2개의 등적과정과 2개의 등엔트로피과정
과정 : 1-2가역 단열(등엔트로피)압축, 2-3가역 정적가열, 3-4가역 단열(등엔트로피)팽창, 4-1가역 정적방열
전기점화기관(불꽃점화기관)의 이상적 사이클이다.
열효율
열효율은 압축비만의 함수이다
열효율은 공급열량과 방출열량, 작동유체의 비열비와 압축비에 의해서 결정된다
열효율은 작동유체의 비열비가 클수록 증가한다
4행정기관은 2행정기관보다 열효율이 높다
카르노사이클의 열효율보다 낮다.
디젤사이클
사바테사이클
브레이튼 사이클
✋N4 냉매순환(압응수팽증)
N9 냉매순환(압응수팽증)
압축기→( 응축기 )→( 수액기 )→( 팽창밸브 )→( 증발기 )→압축기
N6 이상기체
비열
✋N6 폴리트로픽
산소의 정압비열(Cp)
산소의 비열비(k)
공업일(압축일)
절대일(팽창일)
✋N3 스털링 사이클
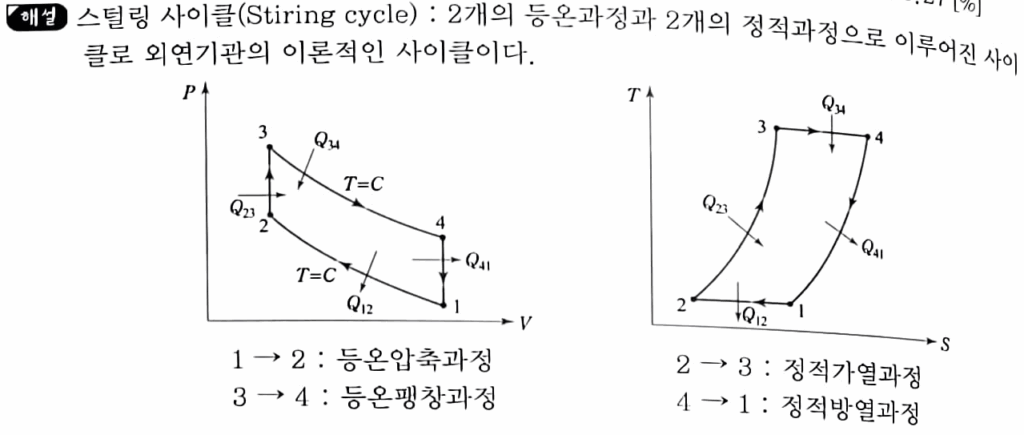
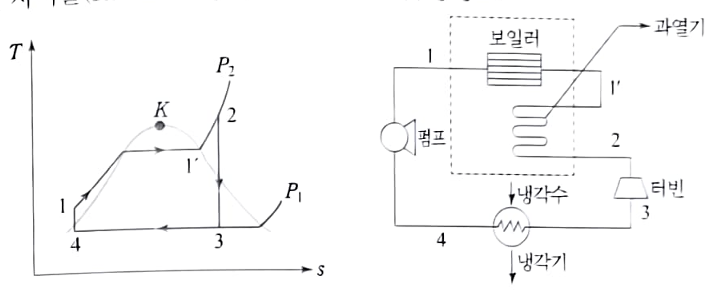
👆N5 습증기엔탈피
N5 습증기엔탈피계산
✋NE 엔트로피의 변화
✋N8 COP
N8 냉동능력, 성능계수(COP)
✋N0 단열압축
기체상수 8.314[kJ /kmol・K]→1.987[kcal/kmol・K] 4.184[J]=1[cal]
N0 단열압축
🔯유체역학 🗄️
🔯유체흐름
관마찰손실(압력손실)
5️⃣ 온도 27[°C], 압력5[bar]에서 비체적이 0.168[m3/kg]인 이상기체의 기체상수 [kJ/kg ·K] 는 얼마인가? (단. 압력은 절대압력이다)
답글 남기기