계산문제 정리
집진장치
4️⃣집진효율
16a11
보일러 집진장치의 입구와 출구의 함진농도를 측정한 결과 각각 50[g/Nm³], 5[g/Nm³]일때 집진효율[%]은 얼마인가
$$ \eta=(\frac{입구농도-출구농도}{입구농도})\times 100\\
=(\frac{50-5}{50})\times100=90[\%] $$
기체상수
5️⃣이상기체상수
16a12
온도 27[°C], 압력5[bar]에서 비체적이 0.168[m³/kg]인 이상기체의 기체상수 [kJ/kg ·K] 는 얼마인가? (단. 압력은 절대압력이다)
이상기체의 기체상수 RR를 단위 질량당(즉, kJ/kg·K 단위로) 구하려면 이상기체 상태방정식과 비체적을 활용할 수 있습니다.
이상기체 상태방정식은
$$ PV=mRT $$
이고, 여기서
P: 압력 [Pa 또는 bar 변환 필요]
V: 부피 [m³]
m: 질량 [kg]
R: 기체상수 [kJ/(kg·K)]
T: 절대온도 [K]
비체적
$$ v=\frac{V}{m} $$
$$Pv=RT$$
따라서,
$$R=\frac{Pv}{T}$$
주어진 값:
온도 T=27∘C=27+273.15=300.15 K
압력 P=5 bar=5×105 Pa (1 bar = 10^5 Pa)
비체적 v=0.168 m3/kg
이 값을 모두 SI 단위로 맞추고 공식에 대입하면,
$$ R=\frac{PV}{mT}=\frac{V}{m}\times \frac{P}{T}=v\times\frac{P}{T} $$
$$ =0.168\times\frac{5\times10^5}{273+27}=279.9J/kg\cdot k=0.28[kJ/kg K] $$
즉, 기체상수는 약 0.28 kJ/(kg⋅K)0.28kJ/(kg⋅K)입니다.
열전도
16a
안쪽 반지름 55[cm] 바깥 반지름 90[cm]인 구형 고압 반응용기(K=41.87[W/m K]) 내외의 표면온도가 각각 551[K], 543[K]일 때 열손실은 몇[kW]인가
D8 구형용기의 열전도 계산
$$ Q=L\frac{4\pi(T_i-T_o)}{\frac{1}{r_i}-\frac{1}{r_o}} $$
$$ Q=K\frac{4\pi(T_i-T_o)}{\frac{1}{r_i}-\frac{1}{r_o}} $$
$$ =(41.87\times 10^{-3})\times \frac{4\pi(551-543)}{\frac{1}{0.55}-\frac{1}{0.9}}=5.953[kW] $$
18C
배관 외경이 30[㎜]인 길이 15[m]의 증기관 에 두께 15[㎜]의 보온재를 시공하였다 관 표면온도 100[℃], 보온재 외부온도 20[℃]일 때 단위 시간당 손실열량은 몇[kJ]인가? (단, 보온재의 열전도율은 0.2093[kJ/m·h·℃]이다.)
D8 전도열계산(중공원통)
$$ F_m=\frac{2\pi L(r_o-r_i)}{\ln\frac{r_o}{r_i}} $$
보온재 피복 후 외측 반지름 및 강관 외측 반지름 계산
$$ r_o=\frac{0.03}{2}+0.015=0.03[m] \\ r_i=\frac{0.03}{2}=0.015[m] $$
보온관 표면적 계산(대수평균면적)
$$ F_m=\frac{2\pi L(r_o-r_i)}{\ln\frac{r_o}{r_i}} $$
$$ =\frac{2\pi\times15\times(0.03-0.015)}{\ln\frac{0.03}{0.015}}=2.039\simeq2.04 $$
방열량 계산
$$ Q=K\times F\times \Delta t $$
$$ =\frac{1}{\frac{15}{0.2093}}\times 2.04\times (100-20)=2277.184[kJ/h] $$
지름2[㎜], 길이 10[m] 전선에 전류 10[A], 전압 9[V]로 흐를 때 전선 내부와 플라스틱 피복 사이의 온도(tm)는 얼마인가?
(단, 외기 온도는 30[°C] 상태로 일정하며 플라스틱피복제는 두께 1[㎜], 표면 열전달계수(α) 15[W/m²·K], 열전도율 (λ) 0.15[W/m²·K]이며, 전선에서 발생되는 열량은 모두 외부로 방출된다.)
D8 전도열계산(중공원통)
$$ F_m=\frac{2\pi L(r_o-r_i)}{\ln\frac{r_o}{r_i}} $$
►전선에서 발생되는 열량
$$ Q=E\times I=9\times 10=90[J/s]=90[W] $$
$$ F_m=\frac{2\pi D(r_o-r_i)}{\ln\frac{r_o}{r_i}}=\frac{2\times\pi\times10\times(0.002-0.001)}{\ln\frac{0.002}{0.001}}=0.090[m^2] $$
$$ Q=KF_m\Delta T=\frac{1}{\frac{b}{\lambda}+\frac{1}{\alpha}}\times F_m\times(T_m-T_\alpha) $$
$$ T_m=T_\alpha+\frac{Q}{\frac{1}{\frac{b}{\lambda}+\frac{1}{\alpha}}\times F_m} \\ =273+30)+\frac{90}{\frac{1}{\frac{0.001}{0.15}+\frac{1}{15}}\times 0.09}=376.33[K]-273=103.333[] $$
16a
두께 20[㎜]강관에 스케일이 3[㎜] 부착하였을 때 열전도 저항은 초기상태인 강관의 몇 배에 해당되는가?
D8 다층벽 열전도열 계산
\[Q=\frac{1}{\frac{b_1}{\lambda_1}+\frac{b_2}{\lambda_2}+\frac{b_3}{\lambda_3}}\cdot F\cdot\Delta t\]
강관의 열전도저항
$$ R_1=\frac{b}{\lambda}=\frac{0.02}{40}=0.0005[m^2K/W] $$
스케일의 열전도저항
$$ R_2=\frac{b_2}{\lambda_2}=\frac{0.003}{2}=0.0015[m^2K/W] $$
강관과 비교한 열전도저항비
$$ =\frac{0.0005+0.0015}{0.0005}=4배 $$
18a
어느 공장에서 가동하고 있는 기계의 발생열을 제거하기 위하여 냉동기와 공조기를 이용하여 냉방을 하고 있다. 겨울철에 공조기의 외기(OA) 댐퍼를 40[%]에서 70[%]로 변경하여 외기도입을 증가시켰더니 [보기]와 같은조건으로되었을때 냉동기부하 감소량[kW]은 얼마인가?
공조기 송풍량 : 50000[㎥/h]
개선 전 : 실내온도 24[℃], 상대습도 60[%], 엔탈피 11.7[kJ/kg]
개선 후 : 실내온도 22[℃], 상대습도 60[%], 엔탈피 10.2[kJ/kg]
외기온도 : 20[℃]
공조기 년간 가동시간 : 3393[h]
공기의 밀도 : 1.24[kg/㎥]
D6 열의 이동
공조기 외부 급기 댑퍼를 40[%]에서 70[%]로 변경하면 외기 도입양은 공조기 동풍량의 30[%]에 해당 하는 양이 증가 하는 것 이고, 증가되는 공기량(단위:질량)에 개선 전후의 엔탈피 차에 해당하는양 만큼 냉동기의 부하가 감소된다
부하 감소량= 공기 질량 x 댐퍼개도 증가량 x 엔탈피 차
= (50000 X 1.24) X (0.7-0.4) / (11.7-10.2)=27900[kcal/h]
16B 17B14 17C12
내벽은 내화벽돌로 두께 20[cm] 열전도율이1.3[W/m℃], 외벽은 플라스틱절연체로 두께 10[cm], 열전도율이 0.5[W/m℃]로 되어 있는 노벽이 있다. 노 내부의 온도가 500[℃], 외부의 온도가 100[℃]일 때 물음에 답하시오.
(1) 단위 연적당 전열량[W]을 구하시오
D7 열전도율계산
\[Q=K\cdot F\cdot\Delta T \\ =\frac{1}{R_1+\frac{b}{\lambda}+R_2}\times F\times\Delta T \]
b 벽의두께, λ 열전도율, F 표면적
(1) 단위 연적당 전열량[W]을 구하시오
\[Q=K\cdot F\cdot\Delta t \]
\[=\frac{1}{\frac{b_1}{\lambda_1}+\frac{b_2}{\lambda_2}}\times F\times \Delta t \\ \]
\[=\frac{1}{\frac{0.2}{1.3}+\frac{0.1}{0.5}}\times 1\times400=1130.43[W]\]
(2) 내화벽돌과 폴라스틱 절연체가 접촉되는 부분의 온도 [℃]를구하시오.
$$ Q=\frac{1}{\frac{b_1}{\lambda_1}}\times F\times \Delta t $$
$$ (t_2-t_0)=Q\times\frac{b_1}{\lambda_1} $$
$$ 500-t_0=1130.43\times\frac{0.2}{1.3} \\ t_0=325.99 $$
1️⃣8️⃣ 전도열계산(다층벽)
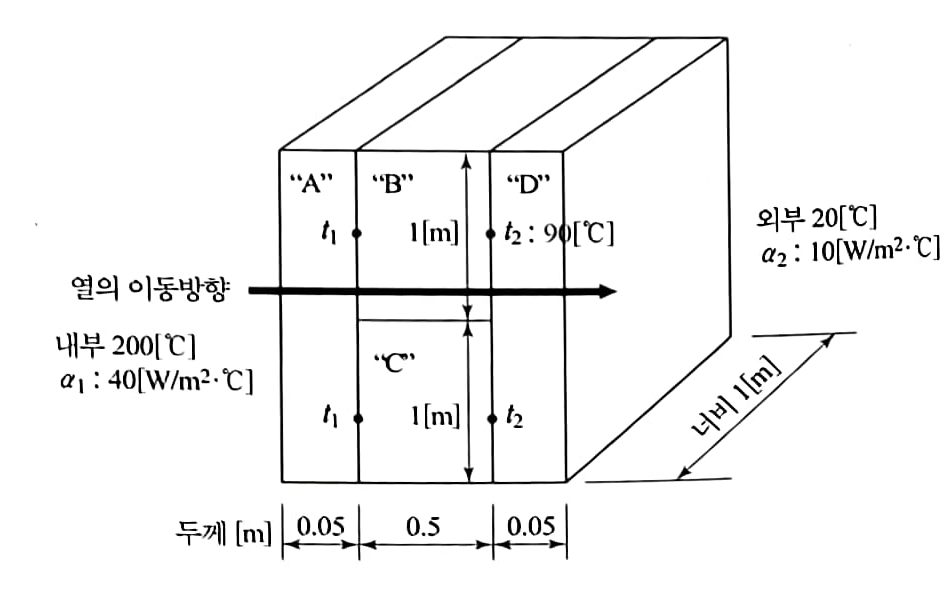
내부온도 200[℃], 외부온도 20[°C]인 곳에 열전도율이 각각 다른 “A”, “B”, “C”, “D”재료로 그림과 같이 3중 구조체가 설치되었고, 구조체의 중간 부분은 “B”와 “C”가 2단으로 구성되어 있다. 이때 “B’’와 “D”의 경계면 온도가 90[℃]로 측정되었을 때 “A”의 열전도율[W/m·°C]을 계산하시오.
(단, “B”, “C”, “D” 열전도율은 각각 10[W/m·℃], 5[W/m·℃], 1[W/m·℃]이고, 내부의 표면 열전달률은 40[W/㎡·K], 외부의 표면 열전달률은 10[W/㎡·K]이고, “A”와 “B”, “C”가 만나는 면의 온도(t₁)와”B”, “C”와 “D”가 만나는 면의 온도(t₂)는 각각의 면 전체에 동일한 것으로 하며, 열 이동 은 상하로는 없고 좌에서 우로 직선 방향으로만 이동하는 것으로 한다.)
D8 다층벽 열전도열 계산
\[Q=\frac{1}{\frac{b_1}{\lambda_1}+\frac{b_2}{\lambda_2}+\frac{b_3}{\lambda_3}}\cdot F\cdot\Delta t\]
$$ Q=K\times F\times \Delta T $$
$$ Q=\frac{1}{\frac{b_1}{\lambda_1}}\times F\times \Delta T $$
$$ Q_2=\frac{1}{\frac{b_D}{\lambda_D}+\frac{1}{\alpha_2}}\times F\Delta t” \\ =\frac{1}{\frac{0.05}{1}+\frac{1}{10}}\times(2\times 1)\times (90- 20) \\ =933.333 $$
$$ \lambda_{(B+C)_m}=\frac{10+5}{2}=7.5[W/mC] $$
$$ Q_1=\frac{1}{\frac{1}{\alpha_1}+\frac{b_A}{\lambda_A}+\frac{B_{(B,C)}}{\lambda_{(B,C)}}+\frac{b_D}{\lambda_D}+\frac{1}{\alpha_2}}\times F\times \Delta t’ $$
$$ \lambda_A=\frac{b_A}{\frac{F\times\Delta t’}{Q_1}-\{\frac{1}{\alpha_1}+\frac{B_{(B,C)}}{\lambda_{(B,C)_m}}+\frac{b_D}{\lambda_D}+\frac{1}{\alpha_2}\}} $$
$$ =\frac{0.05}{\frac{(2\times 1)\times(200-20)}{933.33}-\{\frac{1}{40}+\frac{0.5}{7.5}+\frac{0.05}{1}+\frac{1}{10}\}} \\ =\frac{0.05}{\frac{(2\times 1)\times(200-20)}{9.33.33}-\frac{29}{120}}=0.347 $$
18. 22B
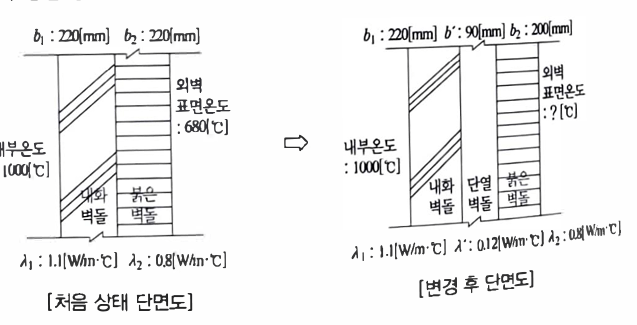
내부온도가 1,000[℃]인 곳에 열전도율 1.1[W/m·℃]인 내화벽돌로 두께 220[㎜] 내벽을 설치하고, 열전도율 0.8[W/m°C]인 붉은 벽돌로 두께 200[㎜]의 외벽을 설치하는 것으로 설계했을 때 외벽의 표면온도가 680[°C]로 예상되었다.
이 상태에서는 열손실이 많이 발생하는 것으로 판단되어 내벽과 외벽 사이 중간에 열전도율이 0.12[W/m·℃]인 단열벽돌을 90[㎜] 보강하는 것으로 설계를 변경하였을 때 외벽의 표면온도는 몇 [℃]가 되겠는가?
(단, 처음 상태와 나중상태의 벽체에서 전열량은 동일하고 내외벽의 표면 열전달율은 무시하고, 기타 손실은 없고 열은 한 쪽 방항으로만 흐른다고 가정한다.)
D8 다층벽 열전도열 계산
\[Q=\frac{1}{\frac{b_1}{\lambda_1}+\frac{b_2}{\lambda_2}+\frac{b_3}{\lambda_3}}\cdot F\cdot\Delta t\]
\[Q=K\times F\times \Delta t \]
\[Q_1=\frac{1}{\frac{b_1}{\lambda_1}+\frac{b_2}{\lambda_2}}\times F\times \Delta t \]
\[ =\frac{1}{\frac{0.22}{1.1}+\frac{0.2}{0.8}}\times 1\times (1000-680)=711.111[W] \]
\[ Q_2=\frac{1}{\frac{b_1}{\lambda_1}+\frac{b_2}{\lambda_2}+\frac{b_3}{\lambda_3}}\cdot F\cdot (t_2-t_1) \]
\[ 711.11=\frac{1}{\frac{0.22}{1.1}+\frac{0.09}{0.12}+\frac{0.2}{0.8}}\cdot 1\cdot (1000-t_1) \]
\[t_1=146.668\]
18C
외기온도 25[°C]일 때 표면온도 230[°C]인 관 표면에서 방사에 의한 전열량은 자연대류에 의한 전열량의 몇 배 가 되는지 계산하시오.
(단, 방사율은 0.9, 스테판-볼츠만 상수는 5.67×10-8[W/㎡·K], 대류 열전달률은 5.56[W/㎡·K]이다.)
D9 복사전열량
$$ Q_1=\epsilon \sigma(T_1^4-T_2^4) $$
$$ Q=\epsilon\cdot C_b\cdot\{(\frac{T_1}{100})^4\cdot (\frac{T_2}{100})^4\}\cdot F_1 $$
D9 대류전열량
$$ Q_2=\alpha\times (T_1-T_2) $$
● 관 표면적 1[㎡]당 방사 전열량 계산
$$ Q_1=\epsilon \sigma(T_1^4-T_2^4)\{복사전열량\} $$
$$ Q_1=\epsilon C_b\{(\frac{T_1}{100})^4-(\frac{T_2}{100})^4\}(방사전열량) $$
$$ =0.9\times(5.67\times10^{-8})\times\{(\frac{273+230}{100})^4-(\frac{273+25}{100})^4\} \\ =2864.181[W/m^2] $$
● 관표면적 1[㎡]단 대류 전열량 계산
$$ Q_2=\alpha\times(T_1-T_2) $$
$$ =5.56\times\{(273+230)-(273+25)\}=1139.8[W/m^2] $$
● 전열량비교
$$ =\frac{Q_1}{Q_2}=\frac{2864.181}{1139.8}=2.512 $$
측정계기
16A 18A
진공 압력과 게이지압력을 측정할 수 있는 연성계에서 진공압력이 50cmHg일 때 절대압력kgf/cm은 얼마인가?(단 대기압은 760mmHg이다.)
I1 절대압력=대기압-진공압력
$$ 1.0332-(\frac{500}{760}\times 1.0332)=0.353[kgf/cm^2\cdot a] $$
절대압력계산
절대압격=대기압력-진공압력=760-500=260[mmHg]
단위변환
1atm=760mmHg=1.0332[kgf/cm2]이다
$$ =\frac{260}{760}\times1.0332=0.353[kgf/cm^2\cdot a] $$
1️⃣1️⃣정압계산(피토관)
16C13
상온, 상압의 공기유속을 피토관으로 측정하였더니 동압이 100[㎜Aq]이었다 이때 유속[m/s] 은 얼마인가?
I2 정압계산(피토관)
\[ V=\sqrt{2g\frac{P_t-P_s}{\gamma}} \]
\[V=\sqrt{2gh\frac{\gamma_m-\gamma}{\gamma}} \]
\[ \gamma(물의 비중량) : 1000[kgf/m^3] \]
\[ 1[atm]=760[mmHg]\]
\[=10332[mmHO]=101.325[kPa] \]
Pt 전압 Ps정압 γ공기밀도
$$ V=\sqrt{2g\frac{P_t-P_s}{\gamma}} $$
$$ V=\sqrt{2\times9.8\times\frac{100}{1000}} $$
4️⃣정압계산(피토관)
18B
물속에 피토관을 설치하여 측정한 전압이 12[mH₂O], 유속이 11. 71 [m/s]이었다. 이때 정압[kPa]은 얼마인가?
I2 정압계산(피토관)
\[ V=\sqrt{2g\frac{P_t-P_s}{\gamma}} \]
\[V=\sqrt{2gh\frac{\gamma_m-\gamma}{\gamma}} \]
\[ \gamma(물의 비중량) : 1000[kgf/m^3] \]
\[ 1[atm]=760[mmHg]\]
\[=10332[mmHO]=101.325[kPa] \]
Pt 전압 Ps정압 γ공기밀도
$$ V=\sqrt{2g\frac{P_t-P_s}{\gamma}} $$
I2 정압계산(피토관)
$$ 11.71=\sqrt{2\times 9.8\frac{(12\times 1000)-P_s}{1000}} $$
$$ P_s=5003.87[mmH_2O] $$
$$ \gamma(물의 비중량) : 1000[kgf/m^3] $$
I1 압력환산 101324=10332=760
1ATM=1.01325bar=101325Pa =10332kg/cm²=1.033mAq =760mmHg
$$ kPa=\frac{5003.87}{10332}\times 101.325=49.072[kPa] $$
18A12
압력 101.325[kPa], 온도 15[℃]에서 공기의 밀도가 1.225[kg/m]이며, 피토관에 설치된 시차 액주계에서 높이차가 330[mmHg]일 때 공기의 유속[m/s]은 얼마인가?
I2 정압계산(피토관)
\[V=\sqrt{2gh\frac{\gamma_m-\gamma}{\gamma}} \]
$$ =\sqrt{2\times9.8\times0.33\times\frac{13600-1.225}{1.225}}=267.958[m/s] $$
안지름 80[㎜]인 배관에 지름 20[㎜]인 오리피스를 설치하여 공기의 유량을 측정하려 한다. 오리피스 전후의 차압이 120[㎜H₂O] 발생하였을 때 유랑[L/min]을 계산하시오. (단, 물의 밀도는 1000[kg/㎥], 공기의 밀도는 1.5[kg/m ] , 유동계수는 0.66 이다)
I4 오리피스(계산)
교축비계산
$$ m=(\frac{D_2}{D_1})^2 $$
유량계산
$$ Q=C\times A\times \frac{1}{\sqrt{1-m^2}}\times \sqrt{2\times g\times h} $$
교축비 계산
$$ m=(\frac{D_2}{D_1})^2 $$
$$ =(\frac{0.02}{0.08})^2=0.0625=0.06 $$
유량계산
$$ Q=C\times A\times \frac{1}{\sqrt{1-m^2}}\times \sqrt{2gh\times\frac{\gamma_m-\gamma}{\gamma}} $$
$$ =0.66\times(\frac{\pi}{4}\times 0.02^2)\times \frac{1}{\sqrt{1-0.06^2}} \\ \times \sqrt{2\times 9.8\times0.12\times\frac{1000-1.5}{1.5}} \\ \times60\times 1000=493.145[L/min] $$
18A
어느 노즐에서 단열 열낙차가 399[kJ/kg]이고, 노즐 속도계수가 0.893일 때 실제 열낙차는 몇 [kJ/kg]인가?
I5 노즐의속도
$$ w_2=\sqrt{2(h_1-h_2)+w_1^2} $$
$$ w_2=\sqrt{2\frac{k}{k-1}\times RT_1\times\{1-(\frac{P_2}{P_1})^{\frac{k-1}{k}}\}} $$
$$ \phi=\sqrt\frac{(h_1-h_2′)}{(h_1-h_2)} \\ (h_1-h_2′)=\phi^2\times(h_1-h_2) \\ =0.893^2\times399=318.182[kJ/kg] $$
21A
1[MPa], 150[℃]의 압축공기가 단면축소 노즐을 통하여 0.5[MPa] 74[℃] 상태로 등엔트로피 팽창할 때 노즐에서의 분출속도 [m/s]를 계산하시오. (단, 공기의 정압비열(Cp)은1.0053[kJ/kg·K], 입구속도는 무시하고 압력은 절대압력이다.)
I5 노즐의속도
$$ w_2=\sqrt{2(h_1-h_2)+w_1^2} $$
$$ w_2=\sqrt{2\frac{k}{k-1}\times RT_1\times\{1-(\frac{P_2}{P_1})^{\frac{k-1}{k}}\}} $$
공기의 정열비열계산
공기의몰질량(M) : 29, Cv : 정열비열, 기체상수 : R
$$ C_p-C_v=R에서 R=\frac{8.314}{M}[kJ/kg\cdot K] \\ C_v=C_p-R=1.0053-\frac{8.314}{29}=0.71861 $$
$$ k=\frac{C_p}{C_v}=\frac{1.0053}{0.7186}=1.398 $$
$$ w_2=\sqrt{2\frac{k}{k-1}\times R\times T_1\times\{1-(\frac{P_2}{P_1})^{\frac{k-1}{k}}\}} $$
$$ =\sqrt{2\times\frac{1.4}{1.4-1}\times \frac{8.314}{29}\times(273+150)\times \{1-(\frac{500}{1000})^\frac{1.4-1}{1.4}\}} \\ =390.531[m/s] $$
유량계수가 1인 피토 튜브를 공기가 흐르는 직경 400[㎜]의 배관 중심부에 설치하였더니 전압이 80[㎜Aq], 정압이 40[㎜Aq]로 지시되었을 때 평균 유량[㎥/s]을 계산하시오 (단, 공기의 비중량은 1.25[kgf/㎥], 물의 비중량은 1000[kgf/㎥], 평균유속은 배관 중심부 유속의 3/4에 해당한다)
I2 정압계산(피토관)
\[ V=\sqrt{2g\frac{P_t-P_s}{\gamma}} \]
\[V=\sqrt{2gh\frac{\gamma_m-\gamma}{\gamma}} \]
\[ \gamma(물의 비중량) : 1000[kgf/m^3] \]
\[ 1[atm]=760[mmHg]\]
\[=10332[mmHO]=101.325[kPa] \]
Pt 전압 Ps정압 γ공기밀도
$$ V=C\sqrt{2\times g\times \frac{P_t-P_s}{\gamma}} $$
$$ =1\sqrt{2\times 9.8\times \frac{80-40}{1.25}}=25.043[m/s] $$
$$ Q=A\times V $$
$$ Q=\frac{\pi}{4}\times D^2\times( V\times \frac{3}{4})=\frac{\pi}{4}\times 0.4^2 \times (25.04\times\frac{3}{4}) \\ =2.359[m^3/s] $$
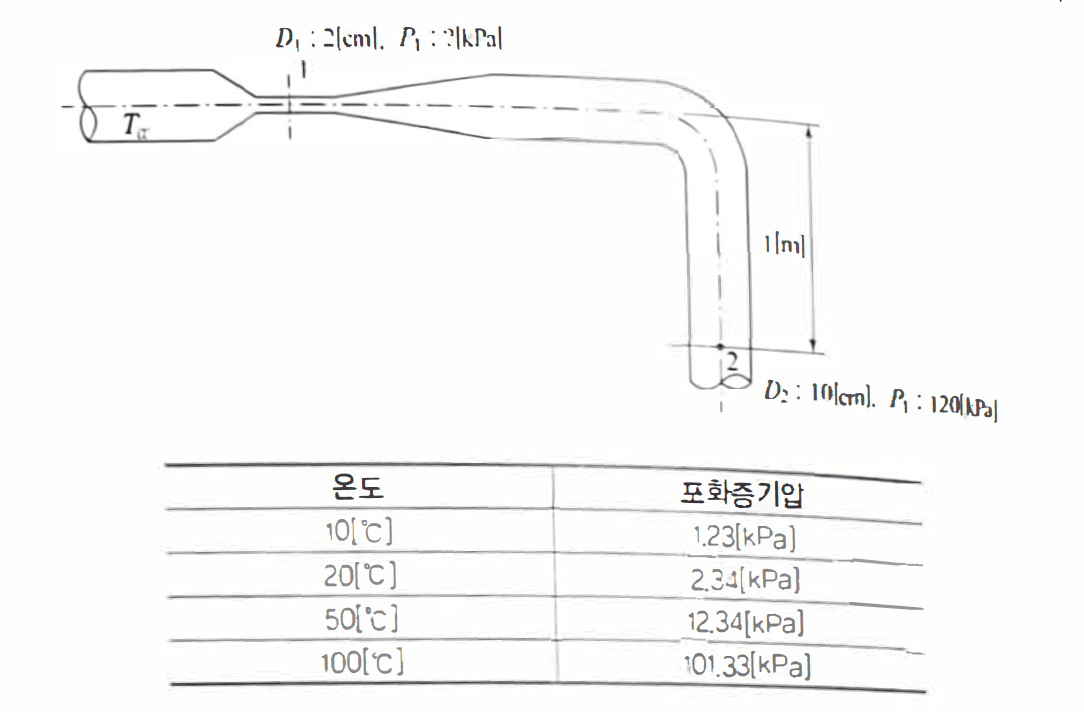
그림과 같은 관로에 벤투리미터를 설치하여 20[°C] 물을 통과시켰을 때 온도기준 포화증기 표를 참고하여 캐비테이션이 발생하지 않는 조건으로 2번 지점에서의 최대유량[L/s]을 계산하시오.
$$ A_1V_1=A_2V_2 \\ V_1=\frac{A_2}{A_1}V_2=\frac{\frac{\pi}{4}\times0.1^2}{\frac{\pi}{4}\times0.02^2}\times V_2=25V_2 $$
$$ \frac{P_1}{\rho g}+\frac{V^2_1}{2g}+z_1=\frac{P_2}{\rho g}+\frac{V^2_2}{2g}+z_2 \\ \frac{V^2_2-V^2_1}{2g}=\frac{P_1-P_2}{\rho g}+z_1 \\ \frac{V^2_2-(25V_2)^2}{2g} =\frac{V^2_2-25^2 V_2^2}{2g} =\frac{V^2_2-625V_2^2}{2g} \\ =\frac{(1-625)V_2^2}{2g}=\frac{-624V_2^2}{2g}$$
$$ \frac{-624V_2^2}{2g}=\frac{P_1-P_2}{\rho g}+z_1 $$
$$ V_2=\sqrt{\frac{2g(\frac{P_1-P_2}{\rho g}+z_1)}{-624}}=\sqrt{\frac{2\times9.8\times(\frac{2000-120000}{1000\times9.8}+1)}{-624}}=0.587[m/s] $$
$$ Q_2=A_2V_2=(\frac{\pi}{4}\times0.1^2\times0.59)\times1000=4.633[L/s] $$
$$ Q_2=A_2V_2=(\frac{\pi}{4}\times 0.1^2\times 0.59)\times 1000=4.633[L/s] $$
$$ V=\sqrt{2g\frac{P_t-P_s}{\gamma}} $$
20A
1기압, 0[°C] 상태의 공기가 원형 덕트에 흐르고 있을 때 원형 덕트 중심부에 피토관을 설치하여 측정한 U자관 마노미터의 눈금이 3[㎜H₂O] 이었다. 이 상태에서 원형 덕트의 지름을 1/2로 축소하면 원형 덕트 중심부의 유속[m/s]얼마인가 (단, 1기압, 0[°C]상태의 공기 밀도는 1.293[kg/㎥]이다.)
I2 정압계산(피토관)
\[ V=\sqrt{2g\frac{P_t-P_s}{\gamma}} \]
\[V=\sqrt{2gh\frac{\gamma_m-\gamma}{\gamma}} \]
\[ \gamma(물의 비중량) : 1000[kgf/m^3] \]
\[ 1[atm]=760[mmHg]\]
\[=10332[mmHO]=101.325[kPa] \]
Pt 전압 Ps정압 γ공기밀도
$$ Q=A_1\times V_1=A_2\times V_2 \\ D_2=\frac{1}{2}D_1 $$
$$ \frac{\pi}{4}\times D_1^2\times V_1=\frac{\pi}{4}\times (\frac{1}{2}\times D_1)^2\times V_2 $$
$$ V_2=\frac{\frac{\pi}{4}\times D_1^2\times V_1}{\frac{\pi}{4}\times (\frac{1}{2}D_1)^2}=\frac{\frac{\pi}{4}\times D_1^2\times V_1}{\frac{\pi}{4}\times \frac{1}{2}^2 D_1^2} \\ =\frac{V_1}{(\frac{1}{2})^2}=4V_1 $$
$$ V=\sqrt{2\times g\times h\times \frac{\gamma_m-\gamma}{\gamma}} $$
$$ V_2=4V_1=4\times\sqrt{2\times g\times h\times \frac{\gamma_m-\gamma}{\gamma}} $$
$$ V_2=\sqrt{2\times 9.8\times 0.003\times \frac{1000-1.293}{1.293}}=26.956[m/s] $$
18A
다음 물음에 답하시오.
(1) 습도계의 종류 3가지를 쓰시오.(단, 건습구 습도계는 제외한다)
(2) 통풍 건습구 습도계로 대기 중의 습도를 측정하였다. 건구온도가 26[℃], 포화수증기 분압 19.82[㎜Hg], 습구온도가 20[℃], 포화수증기 분압 15.47[㎜Hg]일 때 상대습도를 계산하시오.(단. 대기압은 760[㎜Hg]이다)
I8 습도계의종류
모발습도계
전기저항식 습도계
광전관식 노점계
가열식 노점계(듀셀 노점계)
I8 습도계
►수증기분압
\[ P_w=P_{ws}-\frac{P}{1500}\times(t-t’)\]
►상대습도
\[ \phi=\frac{P_w}{P_s}\times 100 \]
►절대습도
\[ X=0.662\times\frac{P_w}{760-P_w} \]
►수증기분압
$$ P_w=P_{ws}-\frac{P}{1500}\times(t-t’) \\ =15.47\times\frac{760}{1500}\times(26-20) \\ =12.43[mmHg] $$
►상대습도
$$ \phi=\frac{P_w}{P_s}\times100 \\ =\frac{12.43}{19.82}\times 100=62.714 $$
2️⃣진공도
18B
직화식 냉온수기에 부착된 U자형 마노미터의 눈금차가 8[㎜Hg]일때 흡수식 냉온수기 내부의 진공도[%]는 얼마인가? (단, 대기압은 760[㎜Hg)이다.)
진공압력 계산
진공압력=대기압상태의 수은주의 높이-액주계 눈금차
진공도 계산
$$ 진공도=\frac{진공압력}{대기압력}\times 100=\frac{752}{760}\times100=98.947 $$
8️⃣비중계산
18B
연료의 비중을 측정하기 위하여 비중계를 비중이 1인 물에 넣었을 때의 수위를 기준점 0으로 하였다. 이 비중계를 연료에 넣었을 때 기준 위 2[㎝]이었다면 이 연료의 비중은 얼마인가? (단, 비중계의 질량 0.04[kg], 비중계 유리관 단면적이 4[㎠]이다)
비중계 상태
물의비중 1,000[kg/㎥]
비중계를 물에 넣었을 때 기준점까지의 거리계산
$$ \rho_1=\frac{m}{V}=\frac{m}{A\times h_1} $$
$$ h_1=\frac{m}{A\times \rho_1}=\frac{0.04}{1000\times\{4\times(10^{-2})^2\}}=0.1[m] $$
연료의 비중 계산
$$ h_2=h_1+2=10+2=2[cm] \\ \rho_1\times h_1=\rho_2\times h_2 \\ s_1\times h_1=s_2\times h_2 \\ s_2=s_1\times\frac{h_1}{h_2} \\ s_2=1\times\frac{10}{12}=0.83 $$
❎1️⃣2️⃣차압계산
18B
그림과 같이 연결된 U자관 마노미터에서 차압[kgf/cm2] Pa- Pb는 얼마인가?
$$ P_A+\gamma_1 h_1=P_B+\gamma_2h_2-\gamma_3h_3+\gamma_4h_4+\gamma_5(h_5-h_4) $$
$$ P_A-P_B=\gamma_2h_2-\gamma_3h_3+\gamma_4h_4+\gamma_5(h_5-h_4)-\gamma_1h_1 $$
$$ =\{(13.6\times 10^3\times 1.14\}-\{(1.26\times 10^3)\times 0.76\}+\{(13.6\times 10^3)\times 0.89\}$$
$$+{(0.95\times 10^3)\times (1.52-0.89)\}-\{(1\times 10^3)\times 1.78\}$$
$$=25468.9\times 10^{-4} =2.546[kgf/cm^2] $$
1️⃣8️⃣유량계산
20C
내경 20[cm]인 원형관에 비중 0.9인 액체가 펌프에서 토출압력 120[kPa] 속도 2[m/s]로 5[m] 높이로 송출 되고 있다. 흡입으로부터 최종 토출구까지 수평거리 15[m], 흡입측에 설치된 연성계의 압력은 완전진공 상태일 때 축동력[kW]을 계산하시오.
(단 펌프의 효율은 90[%], 대기압은 101[kPa] 관마찰계수는 0.02, 엘보 및 밸브의 관상당길이는 각각 1.5, 2이고 관로에는 토출측 밸브만 있는 것으로 가정하고 주어지지 않은 조건은 무시한다)
송출유량 계산
$$ Q=A\times V=\frac{\pi}{4}\times D^2\times V $$
전양정계산(마찰손실계수이용)
$$ h_f=f\times \frac{L}{D}\times \frac{V^2}{2g} $$
축동력 계산
$$ kW=\frac{\gamma \times Q\times H}{102 \times \eta} $$
✋ 마찰손실계수 1️⃣1️⃣ 지름50[㎜], 길이25[m]의 배관에서 마찰손실은 운동에너지의 3.2[%]일 때 마찰손실계수는 얼마인가? (단, 소수점 여섯째 자리까지 구하시오.)
$$ h_f=f\times\frac{L}{D}\times(\frac{V^2}{2g}) $$
❎1️⃣2️⃣
x축의 위치에 따라 지름 D=D₀ /(1+αx)로 변화하는 관에서 x=0일 때 V₀ =4[m/s]이면 x=3에서 유체의 가속도는 얼마인가? (단, 유체는 정상상태, 비압축성이고 상수 α=0.01m-1 이다.)
$$ Q=A\times V $$
$$ V=\frac{Q}{A}=\frac{Q}{\frac{\pi}{4}D^2}=\frac{4Q}{\pi D^2} $$
$$ V_0=\frac{4Q}{\pi D_0^2} $$
$$ D=\frac{D_0}{1+\alpha x} $$
$$ V=\frac{4Q}{\pi D^2}=\frac{4Q}{\pi (\frac{D_0}{1+\alpha x})^2}=\frac{4Q}{\pi (\frac{D_0^2}{(1+\alpha x)^2})}=\frac{4Q}{\pi D_0^2}(1+\alpha x)^2 $$
$$ V_0=\frac{4Q}{\pi D_0^2} $$
$$ V=V_0(1+\alpha x)^2 $$
$$ \alpha=\frac{dV}{dt}=\frac{dx}{dt}\frac{dV}{dt}=\frac{dV}{dx}V \\ 2\alpha\times V_0(1+\alpha x)\times V_0(1+\alpha x)^2=2\alpha V_0^2\times (1+\alpha x)^3 \\ =(2\times 0.01\times 4^2)\times (1+\alpha x)^3=0.32\times (1+\alpha x)^3 $$
8️⃣ 연료비중
19B
연료의 비중을 측정하기 위하여 비중계를 비중이 1인 물에 넣었을 때의 수위를 기준점 0으로 하였다. 이 비중계를 연료에 넣었을 때 기준 위 2[㎝]이었다면 이 연료의 비중은 얼마인가? (단, 비중계의 질량 0.04[kg], 비중계 유리관 단면적이 4[㎠]이다)
비중계 상태
물의비중 1,000[kg/㎥]
비중계를 물에 넣었을 때 기준점까지의 거리계산
$$ \rho_1=\frac{m}{V}=\frac{m}{A\times h_1} $$
$$ h_1=\frac{m}{A\times \rho_1}=\frac{0.04}{1000\times\{4\times(10^{-2})^2\}}=0.1[m] $$
연료의 비중 계산
$$ h_2=h_1+2=10+2=2[cm] \\ \rho_1\times h_1=\rho_2\times h_2 \\ s_1\times h_1=s_2\times h_2 \\ s_2=s_1\times\frac{h_1}{h_2} \\ s_2=1\times\frac{10}{12}=0.83 $$
❎1️⃣2️⃣마노미터
19B
그림과 같이 연결된 U자관 마노미터에서 차압[kgf/cm2] Pa- Pb는 얼마인가?
$$ P_A+\gamma_1 h_1=P_B+\gamma_2h_2-\gamma_3h_3+\gamma_4h_4+\gamma_5(h_5-h_4) $$
$$ P_A-P_B=\gamma_2h_2-\gamma_3h_3+\gamma_4h_4+\gamma_5(h_5-h_4)-\gamma_1h_1 \\ =\{(13.6\times 10^3)\times 1.14\}-\{(1.26\times 10^3)\times 0.76\}+\{(13.6\times 10^3)\times 0.89\}+\{(0.95\times 10^3)\times (1.52-0.89)\}-\{(1\times 10^3)\times 1.78\}=25468.9\times 10^{-4} \\ =2.546[kgf/cm^2] $$
연소계산
17B12
중유를 연소하는 가열로의 연소가스를 분석했을 때 체적비로 CO₂가 15.0[%], CO가 1.2[%], O₂가 8.0[%]이고, 나머지가 N₂인 결과를 얻었다. 이 경우의 공기비를 계산하시오. (단. 연료 증에는 질소가 포함되어 있지 않고, 공기 중 질소와 산소의 부피비는 79:21 이다.)
G2 공기비(m)계산
\[ m=\frac{N_2}{N_2-3.76(O_2-0.5CO)} \]
\[m=\frac{A}{A_0}=\frac{CO_{2max}}{CO_2}=\frac{21}{21-{O_2}} \]
$$ m=\frac{N_2}{N_2-3.76(O_2-0.5CO)} $$
$$ =\frac{100-15-1.2-8}{75.8-3.76(8-(0.5*1.2))}=1.579=1.58 $$
3️⃣[CO₂]max
18B
연도가스 분석 결과 CO₂ 13.5[%], O₂ 7.04[%], CO 0.0[%]이라면 [C0₂]max는 몇 [%]인가?
G3 [CO₂]max
\[ [CO_2]{max}=\frac{CO_2}{G{0d}}\times 100=\frac{21(CO_2+CO)}{21-O_2+0.395CO} \]
$$ [CO_2]{max}=\frac{CO_2}{G{0d}}\times 100=\frac{21(CO_2+CO)}{21-O_2+0.395CO} $$
프로판 1[Sm³]를 공기 증에서 완전 연소 시 수증기를 포함한 이론 연소가스량[Sm³]을 계산히시오.
(단, 공기 조성은 체적으로 질소 79[%], 산소 21[%]이다.)
C3H8
G0 이론산소량(O₀)
\[O_{0}[Nm/kg]=22.4(\frac{C}{12} +\frac{H-\frac{O}{8}}{4}+\frac{S}{32}) \\ O_0[Nm/kg]=1.867C+5.6(H-\frac{O}{8})+0.7S\]
17A
매탄(CH4) 3[Nm³]를 연소시키는데 필요한 이론공기량은 몇 [Nm³]인가?
G0 이론공기량(A₀)
\[ A_{0}[Nm/kg]=\frac{22.4}{0.21}(\frac{C}{12} +\frac{H-\frac{O}{8}}{4}+\frac{S}{32}) \]
$$ A_0[Nm/kg]=\frac{O_0}{0.21}=8.89C+26.67(H-\frac{O}{8})+3.33S \\ A_0[kg/kg]=\frac{O_0}{0.232}=11.49C+34.5(H-\frac{O}{8})+4.31S $$
22.4:2*22.4=3:x
$$ A_0=\frac{O_0}{0.21}=\frac{3222.4}{22.4*0.21}=28.571=28.57[Nm^3] $$
20A
질량 기준으로 C 85[%], H 12[%], S 3[%]의 조성으로 되어 있는 중유를 공기비 1.3으로 연소할 때에 대한 물음에 답하시오.
(1) 실제 공기량[Nm³/kg]을 계산하시오.
(2) 건연소 가스랑[Nm³/kg]을 계산하시오.
G0 이론공기량(A₀)
\[ A_{0}[Nm/kg]=\frac{22.4}{0.21}(\frac{C}{12} +\frac{H-\frac{O}{8}}{4}+\frac{S}{32}) \]
$$ A_0[Nm/kg]=\frac{O_0}{0.21}=8.89C+26.67(H-\frac{O}{8})+3.33S \\ A_0[kg/kg]=\frac{O_0}{0.232}=11.49C+34.5(H-\frac{O}{8})+4.31S $$
$$ A_0=8.89C+26.67(H-\frac{O}{8})+3.33S $$
G5 건연소가스량(Gd)
\[ G_{0d}=8.89C+21.1(H-\frac{O}{8})+3.33S+0.8N \]
\[ G_d=G+B=G+(m-1)A_0 \]
\[ G_d=(m-0.21)A_0+1.867C+0.7S+0.8N \]
$$ G_d=(m-0.21)A_0+1.867C+0.7S+0.8N $$
👆 상당증발량 9️⃣ 19C
압력0| 2[MPa], 건도가 0.95인습포화증기를 시간당 15[ton]을 발생하는 보일러에서 급수온도가 30[°C]일 때, 상당증발량[kg/h]을 계산하시오 (단, 2[MPa]의 포화수와 건포화증기의 엔탈피는 각각 908.79[kJ/kg], 3704.46[kJ/kg]이고, 30[°C] 급수엔탈피는 125.79[kJ/kg], 100[°C] 포화수가 증발하여 건포화증기로 되는 데 필요한 열량은 2257[kJ/kg]이다)
습포화증기 엔탈피 계산
$$ h_2=h’+(h”-h’)x \\ 908.79+\{(3704.46-908.79)\times 0.95\}=3564.676[kJ/kg] $$
상당증발량 계산
$$ G_e=\frac{G_a(h_2-h_1)}{539\times 4.1868}=\frac{G_a(h_2-h_1)}{100[℃]증발잠열} $$
$$ =\frac{(15\times 10^3)\times(3564.68-125.79)}{2257}=22854.829[kg/h] $$
저위 발열량이 9870[kcaI/kg]인 연료를 시간당 300[kg] 사용하는 증발랑 [kg/h]을 구하시오. (단, 보일러 효율은 70[%]이다.)
C2 상당증발량, 환산증발량
\[G_e=\frac{G_a(h_2-h_1)}{539\times 4.1868}=\frac{G_a(h_2-h_1)}{100[℃]증발잠열}\]
\[=\frac{G_a(h_2-h_1)}{\gamma}\]
$$ \eta=\frac{G_a\times (h_2-h_1)}{G_f\times H_l}\times 100=\frac{539\times (h_2-h_1)}{G_f\times H_l}\times 100 $$
$$ G_e=\frac{G_f\times H_l\times\eta}{539}\times 100=\frac{300\times 9870\times0.7}{539}\times 100=3845.454[kg/h] $$
1️⃣2️⃣상당증발량, 환산증발량
16C HH
[보기]와 같은 조건을 이용하여 증기 발생량[kg/h] 을 계산하시오. (단 보일러 열정산 기준을 적용한다)
급수온도 : 50[℃]
보일러 효율 : 85 [%]
연료의 저위발열량 : 10500 [kcal/Nm²]
고위발열량 : 12000 [kcal/Nm²]발생 증기의 엔탈피 : 663.5 [kcal/kg]
연료 사용량 : 373.9 [Nm³/h]
보일러 전열연적 : 102 [m²]
C2 상당증발량, 환산증발량
\[G_e=\frac{G_a(h_2-h_1)}{539\times 4.1868}=\frac{G_a(h_2-h_1)}{100[℃]증발잠열}\]
\[=\frac{G_a(h_2-h_1)}{\gamma}\]
$$ \eta=\frac{G_a(h_2-h_1)}{G_f\cdot H_h}\times 100 $$
$$ G_a=\frac{G_f\times H_h\times \eta}{(h_2-h_1)}=\frac{373.9\times12000\times0.85}{663.8-50}=6213.391[kg/h] $$
20[°C]이 물 10[kg]을 100[°C] 수증기로 만들 때 필요한 열량[kcal]을 구하시오.
C2 상당증발량, 환산증발량
\[G_e=\frac{G_a(h_2-h_1)}{539\times 4.1868}=\frac{G_a(h_2-h_1)}{100[℃]증발잠열}\]
\[=\frac{G_a(h_2-h_1)}{\gamma}\]
$$ Q_1=CG\Delta t \\ Q_2=G\gamma $$
7️⃣상당증발량, 환산증발량
18B
연소실 용적이 2.5[㎥], 전열면적이 49.8[㎡]인 보일러를 가동하였을 때 연료 사용랑이 197[kg/h], 사용연료의 발열량이 9800[kcaI/kg], 실제 증발랑이 2,500[kg/h] 급수온도 40[°C], 발생증기 엔탈피가 662.4[kcal/kg]일 때 환산 증발배수를 계산하시오.
C2 상당증발량, 환산증발량
\[G_e=\frac{G_a(h_2-h_1)}{539\times 4.1868}=\frac{G_a(h_2-h_1)}{100[℃]증발잠열}\]
\[=\frac{G_a(h_2-h_1)}{\gamma}\]
$$ \frac{G_e}{G_f}=\frac{G_a(h_2-h_1)}{539G_f}=\frac{25000\times(662.4-40)}{539\times197}=14.653 $$
$$ G_o=\frac{G_a(h_2-h_1)}{539\times G_f}=\frac{G_a(h_2-h_1)}{100[℃]증발잠열} $$
100[kPa]에서 발생증기량은 10[kg/s], 포화수 엔탈피 420[kJ/kg], 포화증기 엔탈피 3000[kJ/kg], 증기의 건도가 0.9이다. 물의 증발잠열이 2225[kJ/kg]일 때 증발계수를 계산하시오. (단. 급수 엔탈피는 284[kJ/kg]이다)
C2 상당증발량, 환산증발량
\[G_e=\frac{G_a(h_2-h_1)}{539\times 4.1868}=\frac{G_a(h_2-h_1)}{100[℃]증발잠열}\]
\[=\frac{G_a(h_2-h_1)}{\gamma}\]
►습포화증기 엔탈피 계산
$$h_2=h’+(h”-h’)x$$
$$=420+{3000-420}\times 0.9=2742[kJ/kg]$$
►증발계수 계산
$$=\frac{G_e}{G_a}=\frac{h_2-h_1}{\gamma}=\frac{h_2-h_1}{2225}\\
=\frac{2742-284}{2225}=1.104$$
1️⃣3️⃣ 상당증발량, 환산증발량 13상당증발량이 1.5[t/h]인 보일러에 급수엔탈피 83[kJ/kg], 발생증기엔탈피2276[kJ/kg]일때 실제증발량을 구하시오
C2 상당증발량, 환산증발량
\[G_e=\frac{G_a(h_2-h_1)}{539\times 4.1868}=\frac{G_a(h_2-h_1)}{100[℃]증발잠열}\]
\[=\frac{G_a(h_2-h_1)}{\gamma}\]
$$ G_e=\frac{G_a(h_2-h_1)}{539\times 4.1868} $$
$$ (1.5\times 1000)=\frac{G_a(2276-83)}{539\times 4.1868} \\ =1543.560[kg/h] $$
4️⃣고위발열량계산 19B
탄소 55.0[%], 수소 4.0[%], 황 2.0[%], 산소 10.0[%], 질소 5.0[%] 나머지 성분은 회분인 조성을 갖는 석탄의 고위발열량[kJ/kg]은 계산하시오.
(단, 탄소의 발열량 33,858[kJ/kg], 수소의 발열량 142,120[kJ/kg], 황의 발열량은 10,450[kJ/kg]이다.)
H1 고위발열량계산
$$ H_h=8100C+34000(H-\frac{O}{8})+2500S \\ H_h=H_l+600(9H+w) $$
$$ H_h=33858C+142120(H-\frac{O}{8})+10450S $$
8️⃣발열량 18B
발열량이 9050[kcal/L]인 경유 200[L]에 대한 TOE를 계산하시오. (단 경유의 석유환산계수[TOE/kL]는 0.905 이다.)
$$ TOE=\frac{200}{1000}\times 0.905=0.181 $$
9️⃣발열량 18B
[보기]의 가연성가스에서 저위발열량이 높은 것에서 낮은 순서로 나열하시오. 보기
(j) CH4 ® C2H2 ® C3H8 @ C2H4
C3H8(23,660)→ C2H4(14,100)→C2H2(13,500)→CH4(10,500)
7️⃣응축수량
18B 18A
급탕탱크에 시간당 공급되는 물 3,000[kg]을 건도가 0.75인 습증기를 이용하여 30[°C]에서 80[°C]로 가열하여 공급할 때 발생되는 응축수량[kg/h]은 얼마인가
(단, 건포화증기 엔탈피는 661[kca|/kg], 포화수 엔탈피는 171.1[kcaI/kg]이고, 습증기의 현열은 고려하지 않는다)
급탕에 필요한 열량
습증기 잠열
$$ 응축수량=\frac{급탕에 필요한열량}{습증기잠열}=\frac{G\times C\times\Delta t}{(h”-h’)\times x} \\ =\frac{3000\times1\times(80-30)}{(661-171.1)\times0.75}=408.246 $$
연료절감율계산 16C10
🔟보온재손실열량
16C11
배관 외경이 30[㎜]인 길이 15[m]의 증기관에 두께 15[㎜]의 보온재를 시공하였다. 관 표면온도 100[℃]. 보온재 외부온도 20[℃]일 때 단위 시간당 손실열량은 몇[kJ]인가? (단. 보온재의 열전도율은 0.2093[kJ/m•h•℃ ]이다.)
강관의 바깥지름,안지름
$$ r_o=\frac{0.03}{2}+0.015=0.03[m] $$
$$ r_i=\frac{0.03}{2}=0.015[m] $$
$$ F_m=\frac{2\pi L(r_o-r_i)}{\ln\frac{r_o}{r_i}} $$
$$ =\frac{2\pi\times 10\times(0.03-0.015)}{\ln\frac{0.03}{0.015}}=1.3597 $$
증기관의 열손실
$$ Q=K\times F\times \Delta t $$
$$ Q=\frac{1}{\frac{0.03}{0.015}}\times 1.3597\times (150-25)=84.98 $$
대수온도차
2️⃣대수온도차
16C14
대항류식 공기 예열기에 240[℃]의 배기가스가 들어가서 160[℃]로 나오고 연소용 공기는 20[℃]로 들어가서 90[℃]로 나올 때 이 공기예열기의 대수평균온도차를 계산하시오
E3 대수온도차
\[\Delta t_m=\frac{\Delta t_1-\Delta t_2}{\ln(\frac{\Delta t_1}{\Delta t_2})} \]
$$ \Delta t_m=\frac{\Delta t_1-\Delta t_2}{\ln(\frac{\Delta t_1}{\Delta t_2})} $$
$$ =\frac{(420-20)-(160-90)}{\ln(\frac{400}{70})}=359.84 $$
18B
냉각수를 이용하여 오일을 냉각시키는 [보기]와 같은 조건의 대항류 열교환기에서 오일을 냉각시키는 전열면적[m]을 계산하시오.
(단, 열교환기 전열벽의 열관류율은 69.78[W/㎡·°C]이다)
E3 대수온도차
\[\Delta t_m=\frac{\Delta t_1-\Delta t_2}{\ln(\frac{\Delta t_1}{\Delta t_2})} \]
오일을 냉각시키는 데 제거한 열량 계산
$$ Q=G\times C\times \Delta t $$
냉각수 출구온도 계산
👍 대수평균온도차 계산
$$ \Delta t_m=\frac{\Delta t_1-\Delta t_2}{\ln(\frac{\Delta t_1}{\Delta t_2})} $$
🥈 오일 냉각면적 계산
$$ Q=\frac{1}{\frac{b_1}{\lambda_1}}\times F\times \Delta t $$
$$ Q=K\times F\times \Delta t $$
대수평균온도차
17A15
총괄 열전달계수를 구하시오
17B15
전열면적
외경 100[mm], 두께 2.5[mm], 직관길이 2[m]인 연관 9개의 전열면적[m²]을 계산하시오.
B7 전열면적(수관)
\[A=\pi DLn=(\pi d+Wa)Ln\]
연관의 내경 계산
$$ D_i=D_o-2t=100-2*2.5=95 $$
$$ A=\pi DLn=\pi\times0.095\times2\times9=5.372=5.37[m^2] $$
👍 D0 단위 면적당 복사 전열량2️⃣ 17C11무한히 큰 평판이 [보기]와 같은 조건으로 서로 평행한 경우 단위 면적당 복사 전열량[W/㎡]은 얼마인가?
고온부의 온도(t₁) : 1000[℃], 복사율복사능 : 0.5
저온부의 온도(t₂) : 500[℃], 복사율복사능 : 0.9
고온부 및 저온부 각각의 평판 면적(F) : 5[㎡]
스테판 볼츠만 상수(σ) : 5.67 x 10-8 [W/㎡•K⁴]
$$ Q=\sigma\times\frac{1}{\frac{1}{\epsilon_1}+\frac{1}{\epsilon_2}-1}\times F\times (T_1^4-T_2^4) $$
$$ =(5.67\times 10^{-8})\times \frac{1}{\frac{1}{0.5}+\frac{1}{0.9}-1}\times 5 \\ \times((273+1000)^4-(273+500)^4) \\ =304712.6638 $$
$$ Q=K\times F\times \Delta t $$
보일러 부속장치
강판 두께가 25[㎜]이고, 리벳의 지름이 50[㎜]이며, 피치 80[㎜]로 한줄 겹치기 리벳 조인트에서 한 피치마다 하중이 1500[kgf] 작용하면 이 강판에 생기는 인장응력 [Kgf/㎜ ²]과 리벳이음 효율[%]을 구하시오.
E9 리벳이음
인장응력계산
\[ \sigma_t=\frac{W}{t\times(P-d)} \]
\[ \eta=(1-\frac{d}{P})\times 100 \]
P : 리벳의피치, d : 리벳의지름
인장응력
$$ \sigma_t=\frac{W}{t\times(P-d)} $$
$$ =\frac{1500}{25\times(80-50)}=2 $$
리벳이음효율
$$ \eta=(1-\frac{d}{P})\times 100 $$
$$ =(1-\frac{50}{80})\times 100=37.5[\%] $$
임시
필요열량계산17A13
증발시키는데 필요한 열량을 구하시오
포화수의 17C14
8️⃣ 레이놀즈수 18C
내경 25[mm]인 원관에 20[℃]물이 임계레이놀즈수 2320으로 흐르고 있을 때 유속[m/s]은 얼마인가? (단, 20[℃] 물에서의 동점성계수는 1.5 X 10 -6[m/s]이다.)
$$ Re=\frac{\sigma DV}{\mu}=\frac{DV}{v} $$
$$ V=\frac{Rev}{D}=\frac{2320\times1.5\times10^{-6}}{0.025}=0.139[m/s] $$
5️⃣ 연돌상부면적 19A
연돌 출구에서 배기가스의 평균온도가 150[℃]이고 출구 가스의 속도가 7.8[m/s]이다. 시간당 12,000[N㎥]의 배기가스가 배출되고 있을 때 연돌의 상부 단면적[㎡]을 구하시오.
배기가스 압력 (Pg)이 주어지지 않았으므로 대기압(760[mmHg])과 같은 것으로 하여 계산에서는생략한다
$$ F=\frac{G(1+0.0037t)\times (\frac{760}{P_g})}{36,00W} $$
$$ =\frac{12000(1+0.0037\times 150)\times (\frac{760}{P_g})}{36,00\times 7.8}=0.664[m^2] $$
👆 F6 통풍력 1️⃣1️⃣ 18B 19B배기가스 평균온도가 200[℃], 비중량 13.27[N/㎥], 외기온도가 20[℃], 비중량이 12.64[N/㎥]인 경우 통풍력이 527[Pa]이다. 이 때 연돌의 높이[m]는 얼마인가?
$$ Z=273H(\frac{\gamma_a}{T_a}-\frac{\gamma_g}{T_g}) $$
$$ H=\frac{Z}{273(\frac{\gamma_a}{T_a}-\frac{\gamma_g}{T_g})} \\ =\frac{527}{273(\frac{12.64}{273+20}-\frac{13.27}{273+200})}=127.968[m] $$
9️⃣터빈출력 20C
과열기 출구압력 10[MPa], 온도 450[℃] 인 증기를 공급받아 처음에 포화증기가 될때까지 고압 터빈에서 단열팽창을 시킨 다음 추기하여 추가한 압력 밑에서 처음의 온도까지 재열(reheating)한 다음 저압 터빈에 다시 유입시켜 4[kPa]까지 단열팽창시키는 사이클에서 시간당 증기 소비량이 500[kg]일 때 터빈 출력[kW]을 계산하시오. (단, 과재열기 출구 엔탈피(h4) 3259.2[kJ/kg], 고압 터빈에서 단열팽창 후 엔탈피(h3) 2801.4[kJ/kg], 재열기 출구 엔탈피(h2) 3372.6[kJ/kg], 저압 터빈에서 단열팽창 후 엔탈피(h5) 2247[kJ/kg], 복수기에서 정압방열 후 엔탈피(h6) 120.33[kJ/kg], 4[kPa]에서의 포화수 비체적은 0.001004[㎥/kg]이다.)
급수펌프를 구동하는데 소비된 열량계산
$$ W_P=h_1-h_6=v’\times (P_2-P_1) $$
$$ =0.001004\times (10\times 10^3-4)=10.035[kJ/kg] $$
고압터빈의 일량 계산
$$ W_{T1}=h_2-h_3 $$
$$ =3259.2-2801.4=457.8[kJ/kg] $$
$$ W_{T1}=h_4-h_5 $$
저압터빈의 일량 계산
$$ =3372.6-2247=1125.6[kJ/kg] $$
터빈 출력 계산
$$ N_T=\frac{m(W_{T1}+W_{T2}-W_P)}{3600} $$
$$ =\frac{500\times(457.8+1125.6-10.04)}{3600}=218.52[kW] $$
1️⃣8️⃣ 20C
내경 20[cm]인 원형관에 비중 0.9인 액체가 펌프에서 토출압력 120[kPa] 속도 2[m/s]로 5[m] 높이로 송출 되고 있다. 흡입으로부터 최종 토출구까지 수평거리 15[m], 흡입측에 설치된 연성계의 압력은 완전진공 상태일 때 축동력[kW]을 계산하시오.
(단 펌프의 효율은 90[%], 대기압은 101[kPa] 관마찰계수는 0.02, 엘보 및 밸브의 관상당길이는 각각 1.5, 2이고 관로에는 토출측 밸브만 있는 것으로 가정하고 주어지지 않은 조건은 무시한다)
송출유량 계산
$$ Q=A\times V=\frac{\pi}{4}\times D^2\times V $$
전양정 계산
$$ h_f=f\times \frac{L}{D}\times \frac{V^2}{2g} $$
축동력 계산
$$ kW=\frac{\gamma \times Q\times H}{102 \times \eta} $$
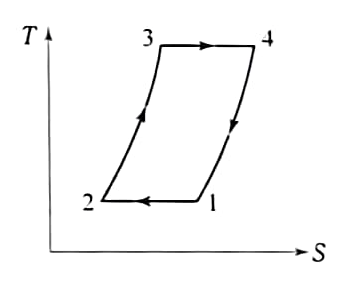
✋ 1️⃣7️⃣ 그림은 스털링 사이클로 작동되는 기관의 온도-엔트로피(T_S) 선도이다 압축비가 6이고, t1 20[℃], t3 1420[℃], Cp 1.0035[kJ/kg·K], Cv 0.718[kJ/kg·K]일 때 물음에 답하시오.
(1) 2 → 3 → 4 과정에서 가열 열량[kJ/kg]을 계산하시오. (2) 4 → 1 → 2 과정에서 방출 열량[kJ/kg]율 계산하시오. (3) 한 사이클당 계가 한 유효일랑[kJ/kg]을 계산하시오. (4) 열효율[%]을 계산하시오.
1️⃣8️⃣ 22C
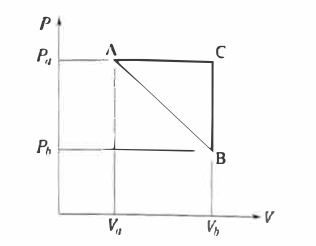
그림과 같이 A→B→C→A 순서로 작동하는 사이클에서 Pa= 300 [kPa]. Pb =200[kPa] va=2[m]이 vb =5[m]가, 외기온도 20[℃]일 때 1사이클에서 한 일[kJ]과 엔트로피 변화(kJ/kg·K]는 얼마인가?
$$ W=\Delta ABC=\frac{1}{2}\times(300-200)\times(5-2)=150[kNm]=150[kJ] $$
$$ \Delta S=C_p\ln(\frac{v_b}{v_a})+C_v\ln(\frac{P_a}{P_b}) \\ =1.006\times \ln(\frac{5}{2})+0.718\times \ln(\frac{300}{200})=1.212[kJ/kgK] $$
1️⃣공기몰수계산*
공기가 채워진 어떤 구형 기구의 반지름이 5[m]이고 내부압력이 100[kPa], 온도는 20[°C]일 때 기구 내에 채워진 공기의 몰수[kmol]를 구하시오.
(단, 공기의 기체상수는 287[J/kg·K]이고, 공기의 분자량은 28.97[g/mol]이다.)
►구형 용기 내용적 계산
$$ V=\frac{4}{3}\pi r^3 $$
$$ V=\frac{4}{3}\pi\times 5^3=523.598 $$
►구형 기구안의 공기 질량 계산
I1 압력환산 101324=10332=760
1ATM=1.01325bar=101324Pa =760mmHg
$$PV=GRT$$
$$ (100+101.325)\times 523.560=G\times 0.287\times (273+20) \\ G=1253.567[kg] $$
►공기 몰수 계산
$$ n=\frac{1253.57}{28.97}=43.271[kmol] $$
연소로로 공기를 공급하는 원심식 송풍기가 970[rpm]으로 회전할 때 축동력이 50[kW]이고, 풍량은 600[m³/min]이다. 연소로의 공기 공급량을 1000[m³/min]으로 증가시킬때 다음 물음에 답하시오. (단. 송풍기 임펠러 직경 크기는 변화가 없다.)
(1) 필요한 송풍기의 회전수[rpm]를 구하시오.
F7 송풍기의 상사
\[Q_2=Q_1\times \frac{N_2}{N_1}\times (\frac{D_2}{D_1})^3(풍량)\]
\[P_2=P_1\times (\frac{N_2}{N_1})^2\times (\frac{D_2}{D_1})^2(풍압)\]
\[L_2=L_1\times (\frac{N_2}{N_1})^3\times (\frac{D_2}{D_1})^5(축동력)\]
$$ Q_2=Q_1\times \frac{N_2}{N_1}\times (\frac{D_2}{D_1})^3 $$
$$ 1000=600\times \frac{N_2}{970} \\ N_2=\frac{970}{600}\times 1000=1616.666 $$
$$ P_2=P_1\times (\frac{N_2}{N_1})^2\times (\frac{D_2}{D_1})^2 $$
$$ L_2=L_1\times (\frac{N_2}{N_1})^3\times (\frac{D_2}{D_1})^5 $$
$$ L_2=50\times (\frac{1616.67}{970})^3=231.482[kW] $$
반지름 20[cm]인 곳에 3[m/s]의 속도로 물이 유입되고 있다. 입구압력 190[kPa], 출구압력 180[kPa]일 때, [보기]의 공식을 이용하여 입구와 출구 사이의 벽면이 받는 마찰력(Ff)[N]을 구하시오.
I5 노즐의속도
$$ w_2=\sqrt{2(h_1-h_2)+w_1^2} $$
$$ w_2=\sqrt{2\frac{k}{k-1}\times RT_1\times\{1-(\frac{P_2}{P_1})^{\frac{k-1}{k}}\}} $$
출구속도
$$ u_2=u_0\{1-(\frac{r}{R})^2\} \\ F_x=P_1A-P_2A-F_f=\frac{dP_{out}}{dt}-\frac{dP_{in}}{dt} $$
출구속도
$$ u_2=u_0\{1-(\frac{r}{R})^2\} \\ =2u_1\{1-(\frac{r}{R})^2\}=2\times3\times\{1-(\frac{0}{0.2})^2\}=6[m/s] $$
$$ \frac{\pi}{4}\times D^2_1\times u_1=\frac{\pi}{4}\times D^2_2\times u_2 $$
출구측 지름계산
$$ D_2=\sqrt{\frac{D^2_1\times u_1}{u_2}}=\sqrt{\frac{0.4^2\times3}{6}}=0.282[m] $$
마찰력계산
$$ F_x=P_1A-P_2A-F_f=\frac{dP_{out}}{dt}-\frac{dP_{in}}{dt}=\rho Q(u_2-u_1) \\ P_1A-P_2A-F_f=\rho Q(u_2-u_1) \\ F_f=P_1A-P_2A-\rho Q(u_2-u_1) \\ =(190\times10^3\times\frac{\pi}{4}\times0.4^2-180\times10^3\times\frac{\pi}{4}\times0.28^2) \\ -\{1000\times(\frac{\pi}{4}\times0.4^2\times3)\times(6-3)\} \\ =11661.591[N] $$
❎ 5️⃣ 길이 2[m], 폭 2[m], 온도 60[°C]인 평판에서 멀리 떨어진 곳에 20[°C]인 유체가 2[m/s]로 평행하게 흐를 때 [보기]의 조건을 이용하여 물음에 답하시오.
(1)열전달계수[W/㎡ K]를 구하시오 (2)전열량[kW]을 구하시오
$$ Re_x=\frac{V_x}{v}=\frac{2\times2}{2\times10^{-4}}=20000 $$
$$ Nu_x=0.3Re^{\frac{4}{5}}P_r^{\frac{1}{3}}=0.3\times20000^{\frac{4}{5}}\times0.8^{\frac{1}{3}}=768.496 $$
$$ h_x=\frac{Nu_x\times k}{x}=\frac{768.50\times0.6}{2}=230.55[W/m^2\cdot K] $$
$$ Q=h_x\times F\times\Delta T=230.55\times(2\times2)\times(273+60)-(273+20) \\ =36888[W]=36.89[kW] $$
어느 공장에서 가동하고 있는 기계의 발생열을 제거하기 위하여 냉동기와 공조기를 이용하여 냉방을 하고 있다. 겨울철에 공조기의 외기(OA) 댐퍼를 40[%]에서 70[%]로 변경하여 외기도입을 증가시켰더니 [보기]와 같은조건으로되었을때 냉동기부하 감소량[kW]은 얼마인가?
공조기 송풍량 : 50000[㎥/h]
개선 전 : 실내온도 24[℃], 상대습도 60[%], 엔탈피 11.7[kJ/kg]
개선 후 : 실내온도 22[℃], 상대습도 60[%], 엔탈피 10.2[kJ/kg]
외기온도 : 20[℃]
공조기 년간 가동시간 : 3393[h]
공기의 밀도 : 1.24[kg/㎥]
D6 열의 이동
공조기 외부 급기 댑퍼를 40[%]에서 70[%]로 변경하면 외기 도입양은 공조기 동풍량의 30[%]에 해당 하는 양이 증가 하는 것 이고, 증가되는 공기량(단위:질량)에 개선 전후의 엔탈피 차에 해당하는양 만큼 냉동기의 부하가 감소된다
부하 감소량= 공기 질량 x 댐퍼개도 증가량 x 엔탈피 차 = (50000 X 1.24) X (0.7-0.41) / (11.7-10.2)=27900[kcal/h]
❎ 1️⃣6️⃣ 17
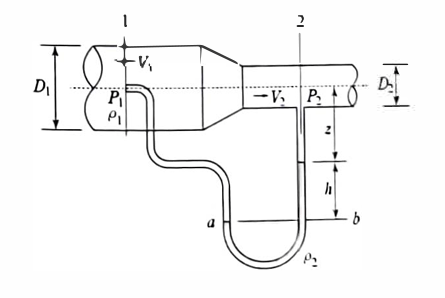
그림과 같이 설치된 피토관에 대한 물음에 답하시오.
(1) 액주계 높이 h를 로 나타내시오.
$$ P_1+\rho_1g(z+h)=P_2+\rho_1gz+\rho_2gh \\ P_1+\rho_1gz+\rho_1gh=P_2+\rho_1gz+\rho_2gh \\ P_1-P_2=\rho_1gz+\rho_2gh-\rho_1gz-\rho_1gh \\ P_1-P_2=(\rho_2g-\rho_1g)h $$
$$ h=\frac{P_1-P_2}{\rho_2g-\rho_1g} $$
$$ \frac{P_1}{\rho_1g}+\frac{V_1^2}{2g}=\frac{P_2}{\rho_1g}+\frac{V_2^2}{2g} \\ \frac{V_2^2}{2g}=\frac{P_1-P_2}{\rho_1g} \\ \frac{V_2^2}{2g}=\frac{(\rho_2g-\rho_1g)h}{\rho_1g}=\frac{(\rho_2g-\rho_1g)}{\rho_1g}h=(\frac{\rho_2g}{\rho_1g}-1)h $$
$$ h=\frac{V_2^2}{2g(\frac{\rho_2 g}{\rho_1 g}-1)} $$
$$ Q=A_1V_1=A_2V_2 \\ \frac{V_2}{V_1}=\frac{A_1}{A_2} \\ \frac{P_1-P_2}{\rho_1g}=\frac{V_2^2-V_1^2}{2g}=\frac{V_1^2}{2g}(\frac{V_2^2}{V_1^2}-1) \\ \frac{P_1-P_2}{\rho_1g}=\frac{V_1^2}{2g}((\frac{A_1}{A_2})^2-1) \\ \frac{P_1-P_2}{\rho_1g}=\frac{V_1^2}{2g}((\frac{D_2}{D_1})^4-1) \\ \frac{P_1-P_2}{\rho_1g}=\frac{(\rho_2g-\rho_1g)h}{\rho_1g}=(\frac{\rho_2g}{\rho_1g}-1)h \\ \frac{V_1^2}{2g}((\frac{D_1}{D_2})^4-1)=(\frac{\rho_2g}{\rho_1g}-1)h $$
$$ h=\frac{\frac{V_1^2}{2g}\{(\frac{D_1}{D_2})^4-1)\}}{\{\frac{\rho_2g}{\rho_1g}-1\}} $$
동체의 안지름이 2500[㎜], 최고사용압력이 1.5[MPa]인 원통보일러 동판의 최소두께[㎜]를 구하시오. (단, 강판의 인장강도 450[N/㎟] 안전율 4.5, 용접부의 이음효율 0.71, 부식여부는 2[㎜], 동체의 증기온도에 대응하는 값(k)은 무시한다)
E 원통보일러 동판의 최소두께
$$ t=\frac{PD}{2\times \sigma_a\times\eta-2P(1-k)}+\alpha $$
$$ =\frac{1.5\times 2500}{2\times\frac{450}{4.5}\times 0.71-2\times 1.5\times(1-0)}=28.978[mm] $$
보일러 보급수 2,000[톤] 중에 용존산소가 9[ppm] 용해되어 있을 때 이를 제거하기위하여 아황산나트륨(Na₂SO₃)은 몇 [kg]이 필요한가?
P6 저온부식
연료 중에 함유된 유황분이 연소되어 (아황산가스(SO₂) )가 되고 이것이 다시 (오산화바나듐(V₂O₅) )의 촉매작용에 의하여 과잉공기와 반응하여 일부분이 (무수황산(SO₃) )이 되고 이것이 연소가스 중의 (수증기(H₂O) )와 화합하여 (급수예열기나 공기예열기 ) 등과 같은 저온의 전열면에 응축되어 황산(H₂SO₄)이 되어서 심한 부식을 일으키는 것이다.
$$ 2000\times10^{6} \times 9\times10^{-6}=18000[g] \\ 2126:32=x:18000 \\ x=\frac{2126*1800}{32}=141750[g] $$
2Na₂SO₃+O₂→Na₂SO₄








답글 남기기