전기기초(회로) AC
전압원, 전류원
2 회로망의 재정리
3 수동소자의 페이저 해석
4 삼각함수 미분
5 순시값 평균값 실효값
최대전력전달
유도결합회로로
8 평형3상회로
9 비정현파 교류
공진현상
과도현상
필터회로
목차(공진현상 ACR)
공진현상
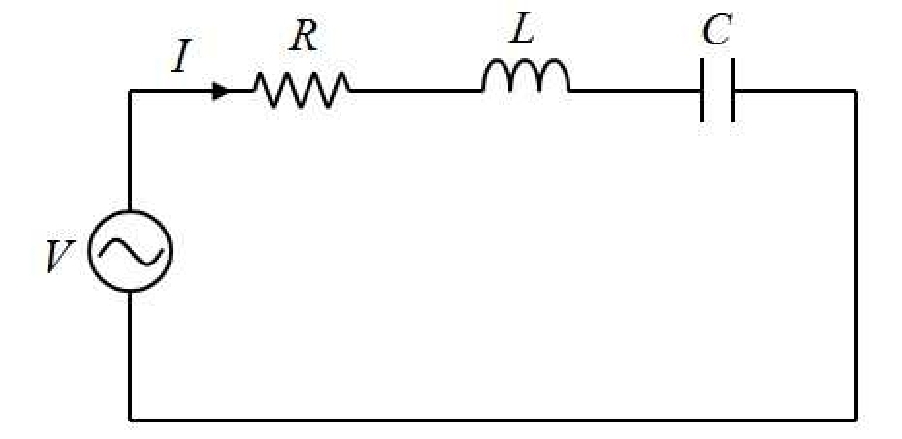
1️⃣직렬공진
(Series Resonance)
- 정의:
- 저항(R), 코일(L), 콘덴서(C)가 직렬로 연결된 회로에서, 코일의 리액턴스(XL (jwL))와 콘덴서의 리액턴스(XC(1/jwC))가 서로 상쇄되어 회로의 임피던스가 최소가 되는 상태를 말합니다.
- 즉, 회로에 흐르는 전류가 최대가 되는 상태입니다.
\[ Z=R+jX=R+j(\omega L-\frac{1}{\omega C})\]
\[=R[\Omega] \]
1)직렬공진 특징
- 임피던스 최소: 회로의 저항 성분만 남아 전류가 가장 잘 흐릅니다.
- 임피던스가 최소
- 전압과 전류가 동상
- 역률이 100[%]
- 전압 확대 가능성
2)임피던스 최소(전류가 최대되는 조건)
\[\dot{V} =\dot{I} \dot{Z} =\dot{I} (R+ j X) \]
\[= \dot {I} ( R + j ( \omega L -\frac { 1} {\omega C} ) ) \]
\[=\dot{ I}R\]
→전압과 전류 동상
3)공진 주파수
(Resonance Frequency)
공진 주파수는 리액턴스 부분이 0이 되어야 하므로 다음 식에 의해 구할수 있다.
\[f_r =\frac { 1} { 2\pi \sqrt { LC} } [Hz]\]
\[ \omega L=\frac{1}{\omega C} \to 2\pi f L=\frac{1}{2\pi fC}\]
\[\to f^2=\frac{1}{(2\pi)^2LC}\]
\[ f_r=\frac{1}{2\pi}\sqrt{\frac{1}{LC}}=\frac{1}{2\pi\sqrt{LC}}[Hz]\]
4) 직렬공진시 L과 C에 걸리는 전압의 확대
(전압 확대비)
\[Q_r = \frac{ \omega_r L} { R}\]
→직렬공진시 콘덴서 및 리액터 과전압에 의한 절연파괴
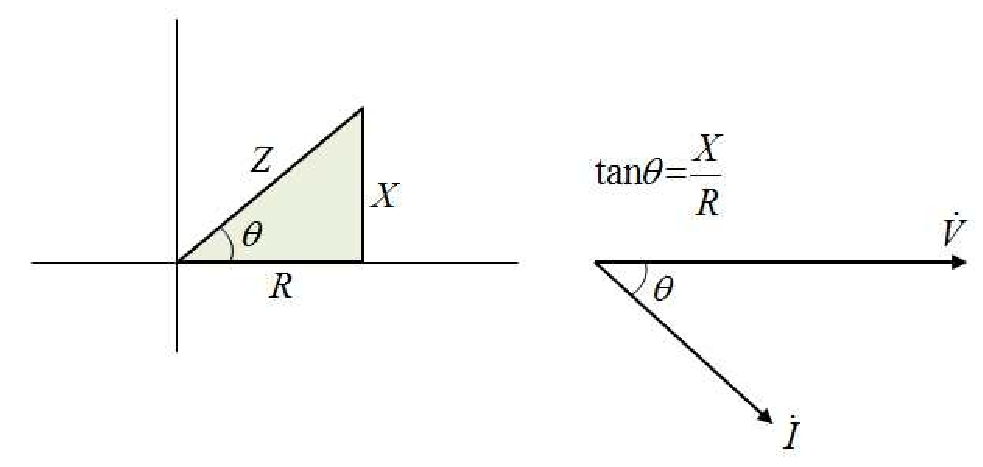
5)임피던스 각
전류가 전압보다 뒤진 경우
\[\dot {Z} =\frac { \dot{V}} {\dot{ I} } =\frac { V \angle0} {I \angle -\theta } = Z \angle \theta\]
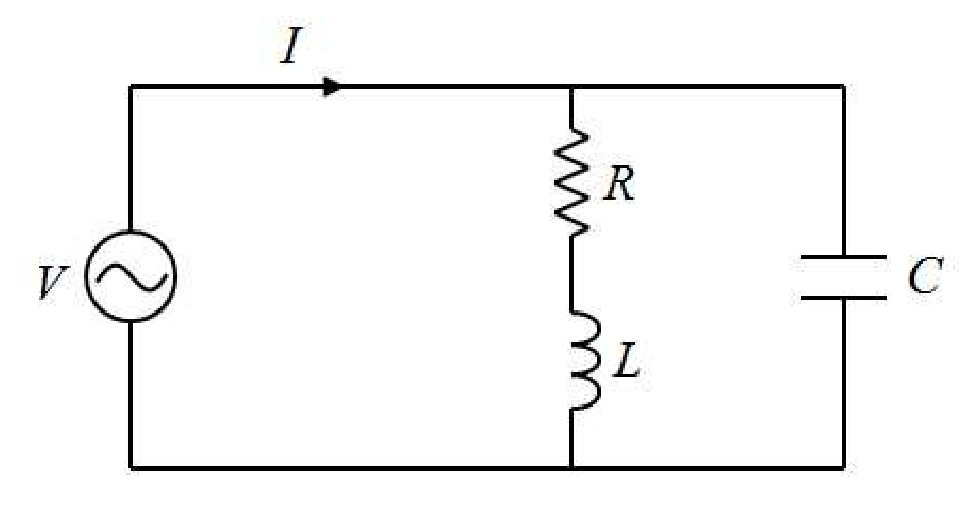
2️⃣병렬공진
(Parallel Resonance)
- 정의:
- 저항(R), 코일(L), 콘덴서(C)가 병렬로 연결된 회로에서, 코일의 리액턴스(XL)(jwL)와 콘덴서의 리액턴스(XC)(1/jwC)가 서로 상쇄되어 회로의 임피던스가 최대가 되는 상태를 말합니다.
- 즉, 회로에 흐르는 전류가 최소가 되는 상태입니다.
\[I=YE\]
\[\omega C=\frac{1}{\omega L}이며\]\[I=j(\omega C-\frac{1}{\omega L})E=0 \]
1)병렬공진 특징
- 어드미턴스가 최소이므로 전류가 최소
- 전압과 전류가 동상
- 역률이 100%
- 전류 확대 가능성
2) 임피던스 최대(전류가 최소되는 조건)
\[\dot{I} =\dot{V} \dot{Y}\]
\[ =\dot{V} (G+jB)=\dot{V} [\frac {R ^{2}} {R ^{2} +( \omega L) ^{2}} +j ( \omega C- \frac{ \omega L} { R^2 +(\omega L)^2 } ) ]\]
\[\dot{Y} = \frac{1}{R+j \omega L} +j \omega C= \frac{R-j \omega L}{R ^{2} +( \omega L) ^{2}} +j \omega C\]
\[= \frac{R}{R ^{2} +(\omega L) ^{2}} +j ( \omega C-\frac{\omega L} {R ^{2} +(\omega L) ^{2}} )\]
→전압과 전류 동상
3)공진주파수
(Anti-Resonance Frequency)
공진주파수는 직렬공진과 마찬가지로 리액턴스 부분이 0 이 되어야 하므로 다음 식에 의해 구할 수 있다
\[ f_a =\frac { 1} { 2\pi \sqrt { LC} } [Hz] …(R \ll \omega _{a} L)\]
\[ \omega L=\frac{1}{\omega C}\to 2\pi fL=\frac{1}{2\pi fC}\]
\[\to f^2=\frac{1}{(2\pi)^2LC}\]
\[ f=\frac{1}{2\pi}\sqrt{\frac{1}{LC}}=\frac{1}{2\pi\sqrt{LC}} \]
상기 식에서와 같이 병렬공진 주파수와 직렬공진 주파수는 식이 같다
4) 병렬 공진시 L 과 C에 흐르는 전류의 확대
\[Q_a = \frac{ \omega_a L} { R}…전류 확대비\]
→고조파 전류에 의한 고조파 전류 계통으로 확대

5)어드미턴스 각
전류가 전압보다 앞선경우
\[\dot {Y}=\frac{\dot{I}}{\dot{V}}=\frac{ I \angle0}{V \angle -\theta } = Y \angle \theta\]
전기기초(회로) AC
전압원, 전류원
2 회로망의 재정리
3 수동소자의 페이저 해석
4 삼각함수 미분
5 순시값 평균값 실효값
최대전력전달
유도결합회로로
8 평형3상회로
9 비정현파 교류
공진현상
과도현상
필터회로
목차(공진현상 ACR)
공진현상
🌐V1006Z24 / ACR
답글 남기기