교류 순시전력
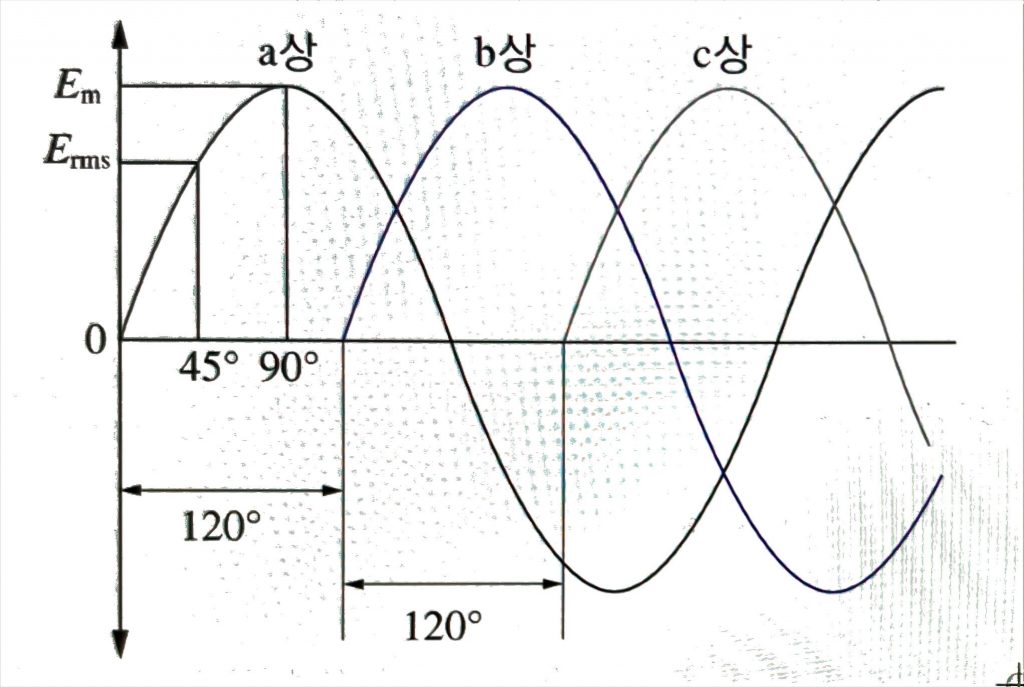
a상의 순시전력
\[ e_a=E_{am}\sin\omega t\]\[ i_a=\sin(\omega t-\theta) \]
\[ p_a=E_{am}I_{am}\sin\omega t\sin(\omega t-\theta)\]\[=2E_aI_a\sin\omega t\sin(\omega t- \theta)\]
\[ =E_aI_a\cos\theta -E_aI_a\cos(2\omega t-\theta) \]
\[여기서/ E_aI_a\cos\theta : 일정한전력 \]
\[E_aI_a\cos(2\omega t-\theta) : \]\[2배의\ 주파수로\ 변하는\ 전력 \]
b상 순시전력
\[ e_b=E_{bm}\sin\omega t-240\]\[ i_b=I_{bm}\sin(\omega t-240-\theta) \]
\[ p_b=E_{bm}I_{bm}\sin\omega t-240\sin(\omega t-240-\theta)\]\[=2E_bI_b\sin\omega t-240\sin(\omega t-240- \theta)\]
\[ =E_bI_b\cos\theta -E_bI_b\cos(2\omega t-480-\theta) \]
c상 순시전력
\[ e_c=E_{cm}\sin\omega t-120\]\[ i_c=I_{cm}\sin(\omega t-120-\theta) \]
\[ p_c=E_{cm}I_{cm}\sin\omega t-120\sin(\omega t-120-\theta)\]\[=2E_cI_c\sin\omega t-120\sin(\omega t120- \theta)\]
\[ =E_cI_c\cos\theta -E_cI_c\cos(2\omega t-240-\theta) \]
순시 전력의 합
\[ P_3=E_aI_a\cos\theta-E_aI_a\cos(2\omega t-\theta)\]
\[ +E_bI_b\cos\theta-E_bI_b\cos(2\omega t-\theta-480)\]
\[ +E_cI_c\cos\theta-E_cI_c\cos(2\omega t-\theta-240)\]
\[=3EI\cos\theta\]
답글 남기기