보호방식의 결정 LP
배선용 차단기(MCCB) DB
누전차단기(ELB) DE
수전설비의 저압선로 보호방식 DL
코로나 DC
코로나(임계전압식 유도)
목차(코로나 임계전압식 유도)
코로나(임계전압식 유도)
코로나 임계전압식 유도
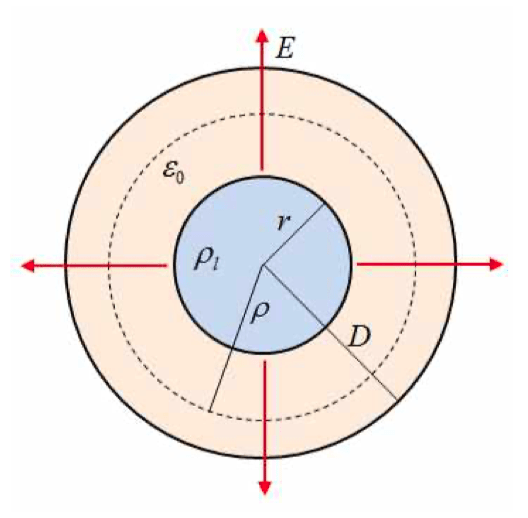
Gauss 법칙에 의한 전계 계산
임의의 폐곡면을 빠져나오는 총 전속은 그 폐곡면 내의 전하량과 같다
\[D=\frac{\psi }{S}=\frac{Q}{2\pi\rho\times l}=\frac{\rho_l}{2\pi\rho}\to E=\frac{\rho_l}{2\pi\epsilon_0\rho}\]
도체의 표면에서 전계, 즉 전계가 최대가 되는 부분이 된다
\[E_{max}=\frac{\rho_l}{2\pi\epsilon_0r}\cdot\cdot\cdot(1)식\]
전위차
+1[C]을 D에서 r까지 옮기는데 소요되는 일
\[V=-\int_D^r Edr=\frac{\rho_l}{2\pi\epsilon_0}[\ln]_r^D=\frac{\rho_l}{2\pi\epsilon_0}ln\frac{D}{r}\]
\[\rho_l=\frac{2\pi\epsilon_0V}{\ln\frac{D}{r}}\cdot\cdot\cdot(2)식\]
전계와 전위차 관계
(2)식 ➔ (1)식 대입
\[E_{max}=\frac{V_{max}}{r\cdot \ln\frac{D}{r}}\]
코로나 임계전압(V₀) 산출
공기의 극한파열 전위경도 = 21.1 [kV/cm]
\[{E}_{\max }=\frac{{V}_{0 }}{r\cdot {\log }_e\frac{D}{r}}=21.1\left[kV/cm\right]\]
\[V_{0 }=21.1\times r\times \log _e\frac{D}{r}=21.1\times r\times \frac{\log _{10}{\frac{D}{r}}}{\log _{10}{e}}\]
\[=21.1\times r\times \frac{\log _{10}{\frac{D}{r}}}{0.43429}=48.6\times r\times \log _{10}{\frac{D}{r}}\]
\[=23.4\times 2r\times \log _{10}{\frac{D}{r}}\ \left[kV\right]\]
\[=24.3\times d\times \log _{10}\frac{D}{r}\left[kV\right]\]
여기에 전선의 표면상태 계수(m0), 일기에 관계하는 계수(m1), 상대공기밀도(δ)를 적용하여 코로나 임계전압을 산출한다.
\[V_0=24.3m_0m_1\delta d \log_{10}\frac{D}{r}[kV]\]
보호방식의 결정 LP
배선용 차단기(MCCB) DB
누전차단기(ELB) DE
수전설비의 저압선로 보호방식 DL
코로나 DC
코로나(임계전압식 유도)
답글 남기기