보호방식(수변전회로) BP
R 수전회로 보호방식
L 저압회로 보호방식
S 저압회로 단락보호
B 저압차단기 보호협조
E 저압회로 지락보호방식
P 보호계전기
T 변압기 보호방식
D 비율차동계전기
M 복합계전기
G GPT적용시 CLR의 목적
U 부족전압계전기(UVR)
R 역전력 계전기(RPR)
Q 고장점 측정
1️⃣머레이 루프법
1)휘스톤 브리지법을 이용한 고장점까지의 거리를 계산하는 원리
2)계산방법
- 지락사고시
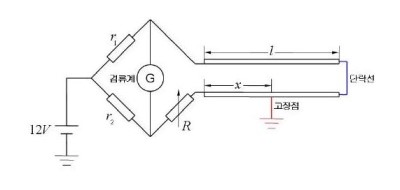
r₁ ,r₂: 머레이루프 저항, R: 가변저항
l:케이블의 긍장, x: 고장점까지의 거리
여기서, 저항은 케이블의 길이에 비례하므로, 길이 l과x를 저항으로 취급한다
\[r_1\times(R+x)=r_2(2l-x)\]
\[x=\frac{(2\times r_2\times l-r_1\times R)}{r_1+r_2}\]
- 선간단락 사고의 경우
\[r_1\times(R+2x)=r_2\times2l\]
\[x=\frac{(2\times r_2\times l-r_1\times R)}{2\times r_2}\]
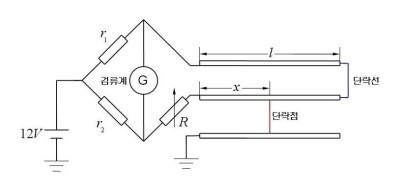
- 특징
측정의 정밀도가 높다
측정 조작 및 운반이 용이하기 때문에 대부분 1선 지락사고 이므로 활용도가 높다
건전상이 없는 3상 단락사고 및 3상 지락사고시에 적용이 불가
지락저항이 높고 사고점이 방전하는경우는 적용이 곤란함
2️⃣펄스레이더법
- 사고 케이블에 펄스 전압을 인가하여 사고점에서 반사되는 펄스파를 감지하여 전파시간을 측정함으로써 사고점까지의 거리를 계산
- 측정원리
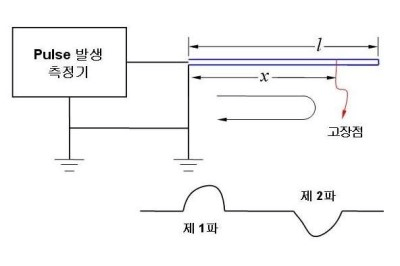
속도=거리/시간 이므로
\[2x=v\times t\]
\[\delta_x=v\times\frac{t}{2}\]
- 특징
- 지락, 단락, 단선 등의 모든 사고에 적용이 가능
- 케이블의 전장이 불투명한 경우에도 적용이 가능
- 측정정밀도가 머레이 루프법보다 뒤진다
- 측정기의 조작 및 판독이 어려워 숙련자만이 다를 수 있다
3️⃣정전 용량법
건전상의 정전용량과 사고상의 정전용량을 비교하여 사고점을 검출하는 방식으로 단선된 경우에만 적용
\[x=l \times\frac{C_x}{C_0}\]
l:케이블의 긍장
4️⃣기타
- 임피던스 브릿지법
- 탐색코일 법
보호방식(수변전회로) BP
R 수전회로 보호방식
L 저압회로 보호방식
S 저압회로 단락보호
B 저압차단기 보호협조
E 저압회로 지락보호방식
P 보호계전기
T 변압기 보호방식
D 비율차동계전기
M 복합계전기
G GPT적용시 CLR의 목적
U 부족전압계전기(UVR)
R 역전력 계전기(RPR)
Q 고장점 측정
💯기출문제
●06 지중케이블의 고장점 추정 방법에 대하여 설명하시오
보호방식(수변전회로) BP
R 수전회로 보호방식
L 저압회로 보호방식
S 저압회로 단락보호
B 저압차단기 보호협조
E 저압회로 지락보호방식
P 보호계전기
T 변압기 보호방식
D 비율차동계전기
M 복합계전기
G GPT적용시 CLR의 목적
U 부족전압계전기(UVR)
R 역전력 계전기(RPR)
Q 고장점 측정
답글 남기기